Was du wissen musst
-
Bei welchen Vierecken gilt der Satz zur Innenwinkelsumme?
Du willst es vielleicht auf den ersten Blick gar nicht glauben, aber der Satz zur Innenwinkelsumme für Vierecke gilt für alle Vierecke, die es gibt.
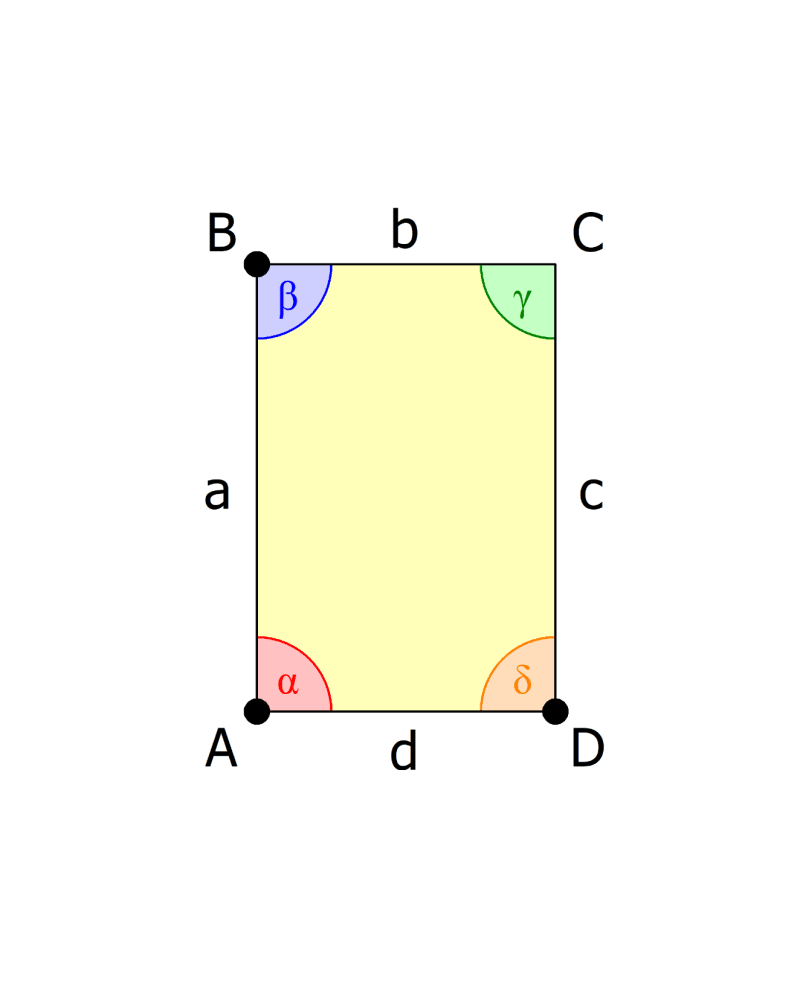
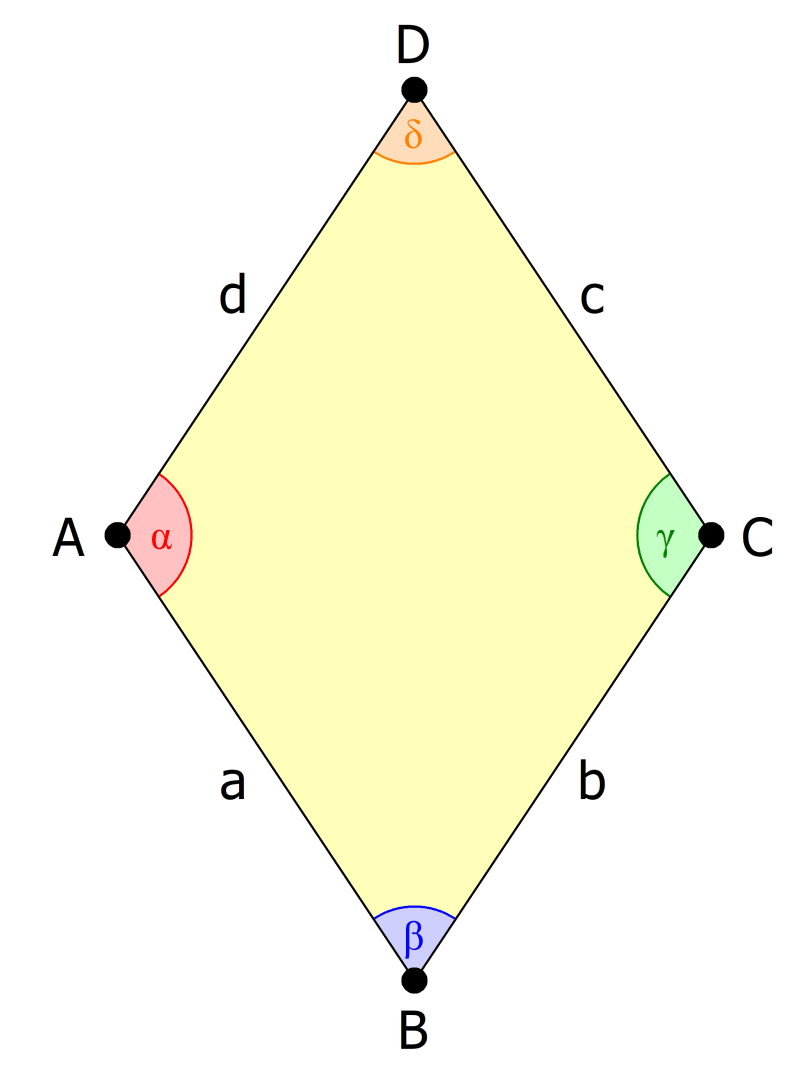
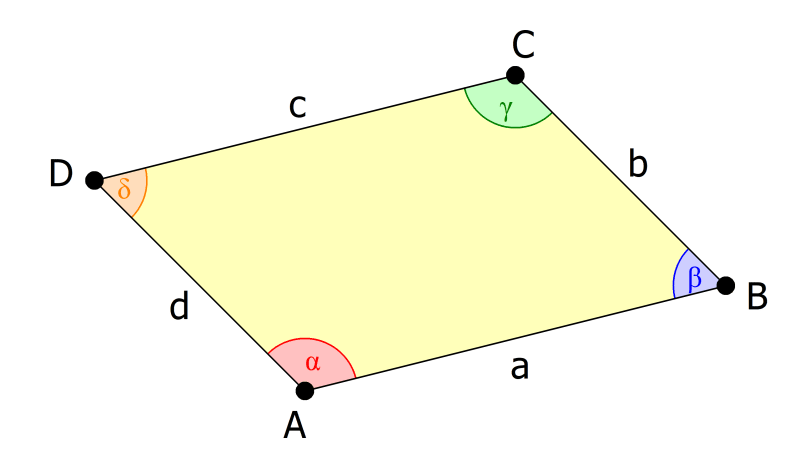
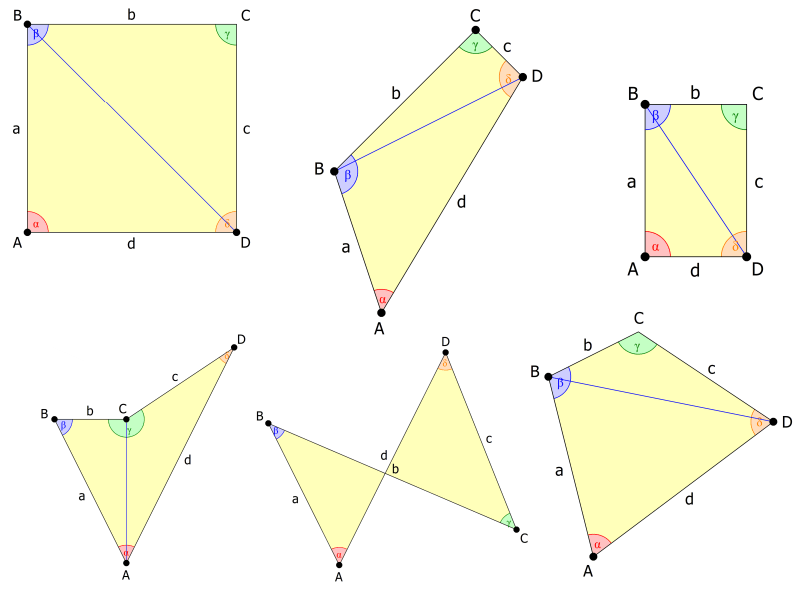
Bei Vierecken mit parallelen Seiten oder auch nur paarweise gleich langen Seiten, wie beim Quadrat, Rechteck, Parallelogramm oder bei der Raute, siehst du das noch auf einen Blick
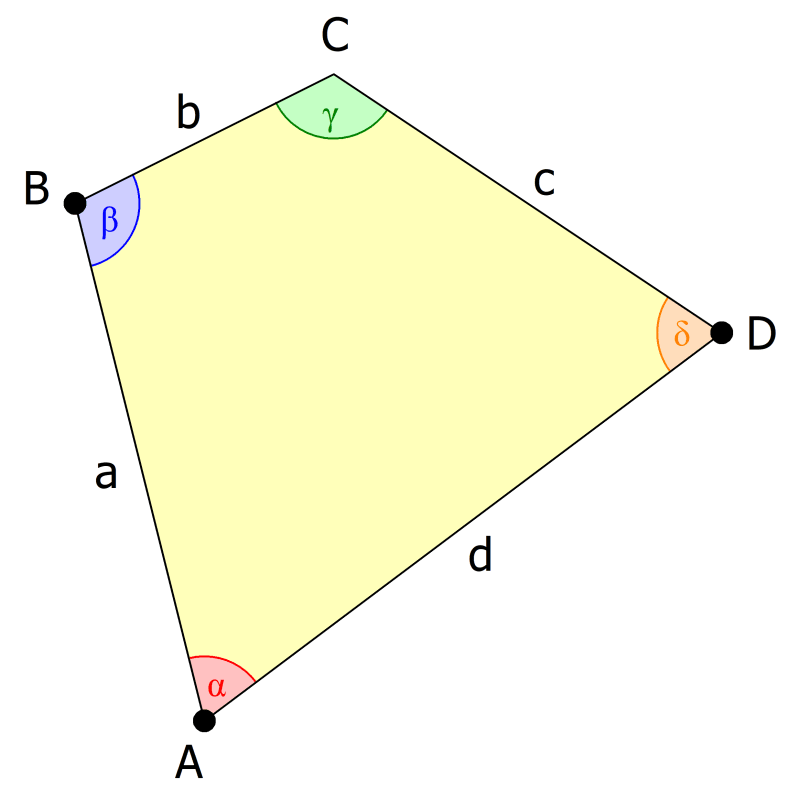
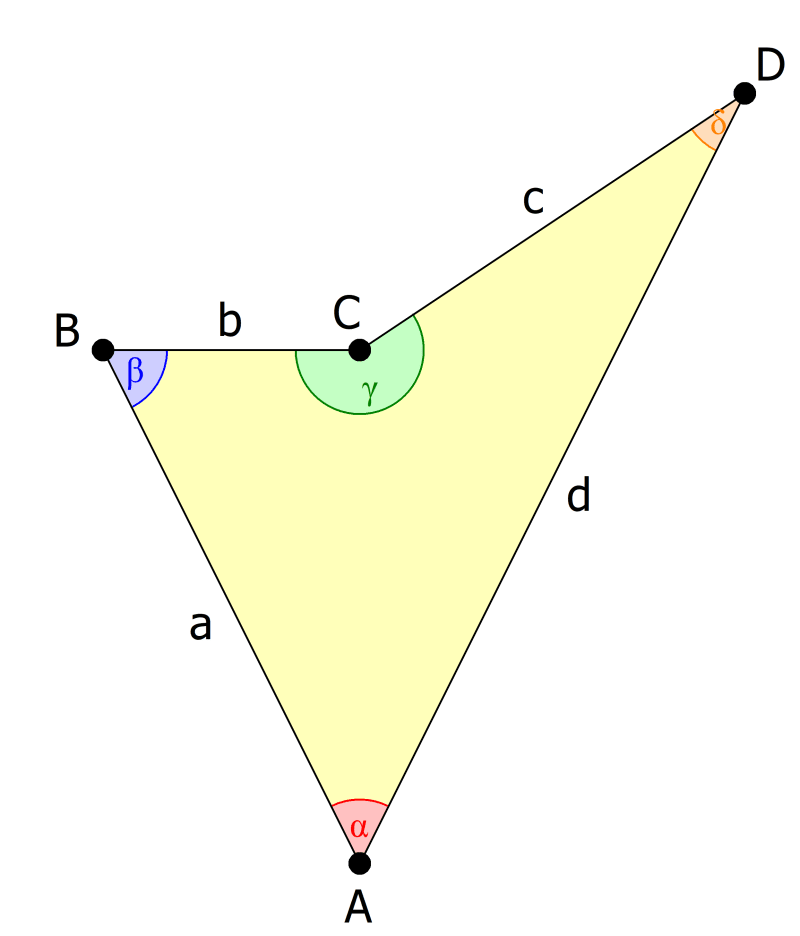
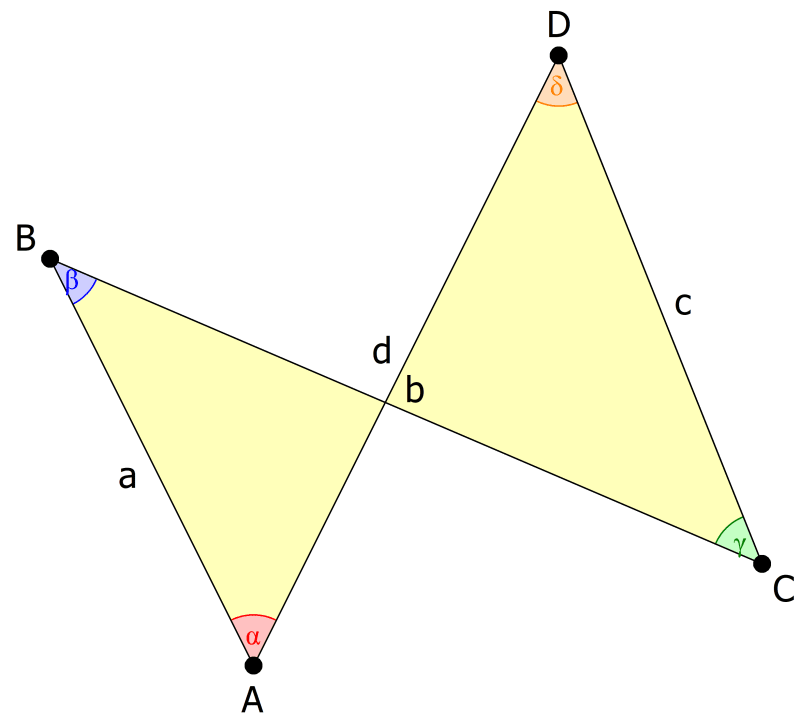
Bei Vierecken, die keine parallelen oder gleich langen Seiten haben, wie konkaven und konvexen Vierecken oder sogar überschlagenen Vierecken, gilt die Innenwinkelsumme auch.
-
Wie kann man den Satz zur Innenwinkelsumme für Vierecke beweisen?
Für den Beweis der Innenwinkelsumme bei Vierecken solltest du den Satz zur Innenwinkelsumme von Dreiecken kennen:
Die Summe der Innenwinkel in einem Dreieck ist immer \(180°\).
Nun ist das auch mit den Vierecken ganz leicht, denn du kannst jedes Viereck in zwei Dreiecke zerlegen, und zwar alle Vierecke, die es gibt.
Jedes Dreieck hat die Innenwinkelsumme von \(180°\). Dann haben zwei Dreiecke zusammen, wenn sie ein Viereck bilden, die doppelte Innenwinkelsumme:
\(180°+180°= 360°\)
Es gibt auch eine allgemeine Form dieser Formel. Du lernst sie bei der Innenwinkelsumme von Vielecken kennen.
-
Wozu braucht man die Innenwinkelsumme von Vierecken?
Durch die Innenwinkelsumme von Vierecken kannst du fehlende Winkel in Vierecken ausrechnen, wenn du die drei anderen Winkel weißt.
Das ist besonders wichtig, wenn es um kompliziertere geometrische Formen geht, die du berechnen musst. Diese Formen kannst du dann in Grundformen wie Dreiecke, Vierecke und Kreise zerlegen und bei diesen Teilfiguren ist es viel leichter, die entsprechende Größen auszurechnen.
Diese Techniken brauchst du nicht nur später in der Schulmathematik, sondern auch, wenn du später einen technischen Beruf erlernen oder zum Beispiel Architektur studieren willst. Auch in deinem Privatleben können dir Probleme mit Winkeln begegnen, zum Beispiel, wenn du eine Einbauküche selber aufbauen willst oder Fliesen selber verlegen möchtest.