Eigenschaften von Körpern

Was du wissen musst

• Welche Gemeinsamkeiten und Unterschiede gibt es bei Körpern?

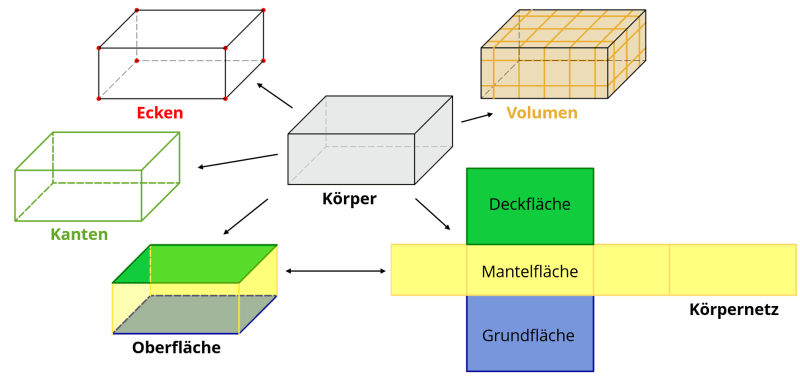
  Nicht alle Körper sind gleich! Ihre Unterschiede kann man auf die verschiedenen Formen zurückführen. Denn die Form eines Körpers bestimmt, wie seine Flächen aussehen. Die Kanten und Ecken ergeben sich aber immer auf die gleiche Weise:

  • Dort, wo die Flächen des Körpers zusammentreffen, entstehen die Kanten.
  • Zusammentreffende Kanten bilden wiederum die Ecken des Körpers.

  Die Oberfläche eines Körpers

  Obwohl die Oberfläche von der Körperform abhängt, gibt es ein paar Gemeinsamkeiten zwischen einer großen Anzahl von Körpern: 

  • Die meisten Körper haben eine Grundfläche, eine Mantelfläche und eine Deckfläche.
  • Die Mantelfläche kann eben oder gekrümmt sein und aus mehreren Teilflächen bestehen.
  • Grund- und Deckfläche können eckig oder kreisförmig ausfallen.

  Es gibt allerdings auch geometrische Körper, die keine Deckfläche haben, wie zum Beispiel eine spitz zulaufende Pyramide.

  Das Volumen eines Körpers

  Weil alle Körper dreidimensionale Objekte sind, nehmen sie einen gewissen Raum ein. Diesen Rauminhalt bezeichnet man mit dem Begriff Volumen. Wie bei der Oberfläche entscheidet die Form und die Größe eines Körpers über sein Volumen.

  

• Welche Formeln für die Eigenschaften von Körpern gibt es?

  Während du an einem geometrischen Körper die Kanten und Ecken abzählen kannst, musst du die Oberfläche und das Volumen eines Körpers berechnen. Dafür gibt es leider keine allgemeine Formel, denn jeder Körper sieht ja unterschiedlich aus.

  Formeln für die Oberfläche

  Auch wenn es keine allgemeine Formel gibt, die die Oberflächen von allen Körpern beschreibt, gibt es einige Oberflächen, die sehr oft vorkommen: Die meisten geometrischen Körper bestehen aus rechteckigen, runden oder dreieckigen Flächen. Wenn du dir die Formeln für den Flächeninhalt dieser Flächen merkst, kommst du schon ein ganzes Stück weiter:

  • Für ein Rechteck mit den Seitenlängen \(a\) und \(b\) gilt für den Flächeninhalt: \(A_{\text{Rechteck}} = a \cdot b\)
  • Den Flächeninhalt eines Kreises mit dem Radius \(r\) berechnest du so: \(A_{\text{Kreis}} = \pi \cdot r^2\)
  • Ein Dreieck mit der Grundseite \(g\) und der Höhe \(h\) hat diesen Flächeninhalt: \(A_{\text{Dreieck}} = \frac{1}{2}\cdot g \cdot h\)

  Formeln für das Volumen

  Auch beim Volumen gibt es nicht die eine Formel für alle Körper. Besonders häufig wirst du aber die Volumenformel für den Quader und den Würfel brauchen:

  \(V = a \cdot b \cdot c \)

  Hier rechnet man also „Länge mal Höhe mal Breite“. Wie das genau funktioniert, kannst du dir in unserem Video zum Volumen eines Quaders anschauen.

• Wozu braucht man die Eigenschaften von Körpern?

  Körper und ihre Formen begegnen uns im Alltag überall. Besonders das Berechnen von Oberflächen hat dabei große Bedeutung. Wenn du zum Beispiel deine erste eigene Wohnung neu streichen möchtest, musst du wissen, wie viel Farbe du benötigst. Weil die Menge der Farbe von der Größe der Wandfläche abhängt, solltest du die Fläche berechnen können. Die geometrische Form eines Zimmers entspricht meistens einem Quader. Die Flächen, die gestrichen werden sollen, entsprechen der Mantelfläche (Wände) und der Deckfläche (Decke). Ähnlich ist es, wenn das Dach neu gedeckt wird und du dich fragst, wie viele Dachziegeln du benötigst. Auch beim Verlegen von Fliesen im Bad oder in der Küche musst du die Fläche kennen.

  Oft hängen auch andere Größen von einer Fläche ab. Wenn deine Familie beispielsweise überlegt, ob es sich lohnt, auf dem Dach eine Solaranlage zu installieren, dann werden die Kosten gegen den Nutzen abgewogen. Der Nutzen ist in diesem Fall der Strom, den die Anlage bereitstellt. Und der hängt von der zur Verfügung stehenden Mantelfläche des Daches ab.

  Außerdem begegnen wir geometrischen Körpern überall in unserer Umwelt: Tische und Bücher haben die Form eines Quaders, Gläser und Blumentöpfe die eines Zylinders und unser Planet hat die Form einer Kugel.

  Auch für die Mathematik selbst sind Körper und Figuren besonders wichtig. Sie sind die Grundlagen der Geometrie, die uns heutzutage vor allem bei allen Arten von Vermessungen helfen.