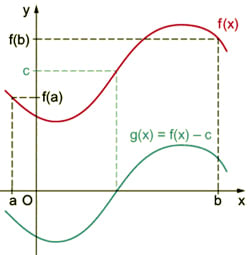
Der Zwischenwertsatz und sein Spezialfall, der Nullstellensatz, sind zwei Sätze über stetige Funktionen. Der Zwischenwertsatz besagt im Wesentlichen, dass eine Funktion keine Werte „auslässt“. Formal lautet er:
- Wenn eine Funktion f in einem abgeschlossenen Intervall [a; b] stetig ist, dann gibt es für jeden Wert y0 zwischen den Funktionswerten der Intervallgrenzen, f(a) und f(b), mindestens ein \(x_0 \in [a; b]\), dessen Funktionswert genau y0 ist: f(x0) =y0.
Das bedeutet:
- Die Zahl y0 ist ein Funktionswert von f.
- 2. Die horizontale Gerade y = y0 schneidet den Graphen Gf.
Ein Sonderfall des Zwischenwertsatzes ist der Nullstellensatz:
- Wenn eine Funktion f in einem abgeschlossenen Intervall [a; b] stetig ist und die Funktionswerte an den Intervallgrenzen, f(a) und f(b), unterschiedliche Vorzeichen haben, dann hat f in [a; b] mindestens eine Nullstelle.
Der Graph Gf schneidet in einem solchen Fall die x-Achse im Intervall [a; b] mindestens einmal.
Beispiel:
Die Funktion f mit \(f (x) = x^5 - 1\) ist stetig im Intervall [0; 3] und es sind f(0) = –1 < 0 und f(3) = 242 > 0. \(f (0) = - 1 < 0, f (3) = 242 > 0\).
Also hat f mindestens eine Nullstelle im Intervall [0; 3].
Anmerkung: Man kann durch Addition oder Subtraktion einer Konstante immer erreichen, dass die Funktionswerte an den Intervallgrenzen unterschiedliche Vorzeichen haben.