Unter einer Verschiebung (auch: Parallelverschiebung oder Translation) versteht man in der Geometrie eine eineindeutige Abbildung, die alle Punkte der Ebene oder des Raums gleich weit und in die gleiche Richtung verschiebt (daher der Name). Wenn man zehn Äpfel alle um genau einen Meter nach Norden verrückt, ist das eine Verschiebung. Würde man einen Apfel nur um 90 cm verrücken oder die Hälfte der Äpfel einen Meter nach Norden, die andere Hälfte aber einen Meter nach Nordwest, wären das keine geometrischen Verschiebungen.
Offensichtlich verändern sich die Abstände zwischen Punkten, Figuren oder Körpern bei einer Verschiebung nicht, deshalb ist die Verschiebung eine (geometrische) Bewegung, in zwei Dimensionen spricht man auch von einer Kongruenzabbildung.
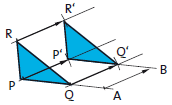
Man kann eine Verschiebung mit einem Vektor eindeutig beschreiben, der Richtung und Entfernung der Verschiebung angibt. Wenn \(\overrightarrow{AB}\) dieser Vektor ist, dann gilt für das Bild \(P'\) von \(P\) unter der Verschiebung, dass die Strecke zwischen \(P'\) und P parallel zu \(\overrightarrow{AB}\) ist, ebenso die Strecke zwischen A und P parallel zur Strecke zwischen B und \(P'\):
\(PP' || AB\) und \(AP || BP'\)