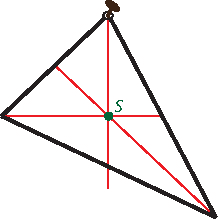
Der Schwerpunkt eines Dreiecks ist der Schnittpunkt seiner Seitenhalbierenden. Wenn die Ortsvektoren der Ecken A, B und C die Vektoren \(\vec a\), \(\vec b\) und \(\vec c\) sind, ist der Ortsvektor des Schwerpunkts \(\displaystyle \vec s = \frac 1 3 (\vec a +\vec b+\vec c)\).
Die Bezeichnung „Schwerpunkt“ kann man auch physikalisch wörtlich nehmen: Wenn man ein dreieckiges Holzbrett (ganz vorsichtig!) auf dem Schwerpunkt balanciert, bleibt es im Gleichgewicht. Und wenn man ein Dreieck an der Spitze drehbar aufhängt, folgt die Verlängerung des Fadens der jeweiligen Seitenhalbierenden (eben weil dann links und rechts gleich viel Dreiecksfläche und damit Gewicht hängt).
Bei einem Parallelogramm ist der Schwerpunkt der Diagonalenschnittpunkt. Sein Ortsvektor ist die halbe Vektorsumme der beiden Vektoren, die das Parallelogramm aufspannen: \(\displaystyle \vec s_\text{Parallelogramm} = \frac 1 2 (\vec a +\vec b)\). Entsprechend ist in drei Dimensionen der Schwerpunktvektor eines Parallelepipeds (Spats) \(\displaystyle \vec s_\text{Spat} = \frac 1 2 \left( \vec a + \vec b + \vec c \right)\).
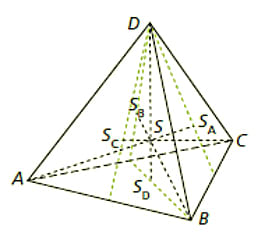
Der Schwerpunkt eines Tetraeders ist der Schnittpunkt der Vebindungslinien zwischen den Ecken und den Schwerpunkten der jeweils gegenüberliegenden dreieckigen Seitenflächen.
Der Schwerpunktvektor ist ein Viertel der Summe der Ecken-Ortsvektoren: \(\displaystyle \vec s_\text{Tetraeder} = \frac 1 4 \left( \vec a + \vec b + \vec c + \vec d\right)\).