Ein Parallelepiped, Parallelflach oder Spat ist ein (im Allgemeinen schiefes) Prisma, dessen Grund- und Deckfläche Parallelogramme sind.
Wenn alle sechs Seitenfläche kongruent sind, heißt der Körper Rhomboeder.
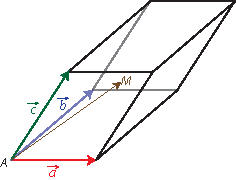
In der Analytischen Geometrie ist ein Parallelepiped der von drei linear unabhängigen Vektoren \(\vec a\), \(\vec b\) und \(\vec c\) aufgespannte Körper.
Sein Volumen lässt sich nach der Prismen-Formel „Grundfläche mal Höhe“ berechnen, V = G · hG. In der Analytischen Geometrie berechnet man dieses Volumen als den Betrag des Spatprodukts der drei Vektoren: \(V = \left| \left( \vec a \times \vec b \right) \cdot \vec c \right| = \det \left( \vec a; \vec b; \vec c \right)\) („det“ steht dabei für die Determinante der Matrix mit den Spaltenvektoren \(\vec a\), \(\vec b\) und \(\vec c\)).
Den Schwerpunkt des Parallelepipeds (Schnittpunkt der Raumdiagonalen) kann man mit der Vektorformel \(\displaystyle \overrightarrow{ AM} = \frac 1 2 \left( \vec a + \vec b + \vec c \right)\) berechnen.