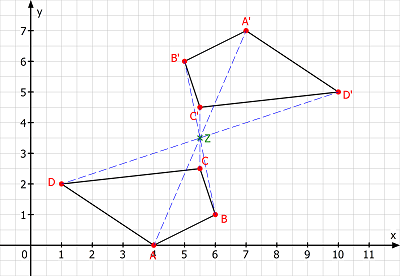
Eine Punktspiegelung ist eine eineindeutige geometrische Abbildung in der Ebene oder im Raum. Man kann sie auf zwei Weisen betrachten:
- entweder als Spiegelung an einem Punkt Z, dem Spiegelzentrum. Für jeden abgebildeten Punkt P (z. B. jede Ecke eines Dreiecks) liegt das Spiegelbild, d. h. das Abbild unter dieser Punktspiegelung, auf einer Geraden durch P und Z, und zwar im selben Abstand, jedoch auf der anderen Seite (siehe Grafik).
- oder als eine Drehung um den Punkt Z, und zwar um den gestreckten Winkel 180° (im Bogenmaß: \(\pi\)).
Formal kann man eine Punktspiegelung an Z so definieren, dass für jeden Punkt P gilt:
- Der Bildpunkt \(P'\) liegt auf dem Kreis um Z durch P und
- \(P'\) liegt auf der Geraden durch P und Z.
Da eine Punktspiegelung also eigentlich nur ein Spezialfall einer Drehung ist, gehört sie genau wie die Drehungen zu den (eigentlichen) Bewegungen bzw. Kongruenzabbildungen. Das bedeutet insbesondere, dass Längen und Winkel bei Urbild und Abbild gleich groß sind und dass die Orientierung einer punktgespiegelten Figur oder eines an einem Punkt gespiegelten Körpers gleich ist. Dies ist bei einer Geradenspiegelung oder bei einer Ebenenspiegelung nicht der Fall.