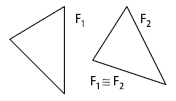
Zwei Figuren sind zueinander kongruent, wenn es eine Abbildung (eine sog. Bewegung oder Kongruenzabbildung) gibt, mit der man die eine Figur mit der anderen zur Deckung bringen kann. Daher sagt man statt „kongruenz“ oft auch „deckungsgleich“. Der Ausdruck Bewegung für eine Kongruenzabbildung ist übrigens ganz wörtlich gemeint: Zwei Dreiecke sind kongruent, wenn sich das eine durch Verschieben oder Drehen so „bewegen“ lässt, dass es das andere exakt abdeckt. Allerdings muss man das Dreieck dafür unter Umständen aus der Ebene herausbewegen: Eine Geradenspiegelung kann man nur dann mit einer realen Bewegung nachmachen, wenn man das Dreieck in der „dritten Dimension“ umkippt.
Wenn zwei Figuren F1 und F2 zueiander kongruent sind, schreibt man dafür \(F_1 \equiv F_2\).
Kongruente Figuren stimmen in Größe und Form überein: Umfang, Flächeninhalt, Seitenlängen, Innen- und Außenwinkel, Höhen usw. - alles außer dem Ort, an welchem sie sich befinden, ist gleich.
Kongruenz ist unempfindlich gegen Verschiebung, Spiegelung, Drehung, wird aber zerstört durch vergrößern und verkleinern, außerdem durch Dehnen, Stauchen, Biegen, Zerren.
Da man alle Figuren zumindest annähernd aus Dreiecken zusammensetzen kann (und Polygone sogar exakt), spielt die Kongruenz von Dreiecken eine besondere Rolle in der Geometrie.