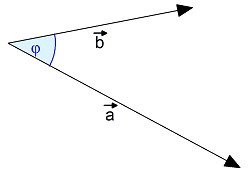
Unter dem Skalarprodukt zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man den Skalar (die reelle Zahl) \(\overrightarrow{a}\circ\overrightarrow{b}=|\overrightarrow{a}|\cdot|\overrightarrow{b}|\cdot\cos\varphi,\) wobei \(\varphi\) der Winkel zwischen den Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist (mit 0° \(\le\varphi\le\) 180°). Aus dieser Definition geht hervor, dass bei aufeinander senkrecht stehenden Vektoren das Skalarprodukt verschwindet (cos 90° = 0), bei parallelen Vektoren ist es maximal groß und entspricht dem Produkt der beiden Vektorbeträge.
Eine weitere wichtige Formel zur Berechnung des Skalarprodukts lautet \(\overrightarrow{a}\circ\overrightarrow{b}= \sum_i a_i \cdot b_i\), in Komponentenschreibweise bedeutet das
\(\pmatrix{a_1\\a_2}\circ\pmatrix{b_1\\b_2}=a_1\cdot b_1+a_2\cdot b_2\) bzw.
\(\pmatrix{a_1\\a_2\\a_3}\circ\pmatrix{b_1\\b_2\\b_3}=a_1\cdot b_1+a_2\cdot b_2+a_3\cdot b_3\)
Für Vektoren \(\overrightarrow{a},\overrightarrow{b}\) und \(\overrightarrow{c}\) und reelle Zahlen r gelten
- Das Kommutativgesetz: \(\overrightarrow{a}\circ\overrightarrow{b}=\overrightarrow{b}\circ\overrightarrow{a}\)
- Das Distributivgesetz: \(\overrightarrow{a}\circ(\overrightarrow{b}+\overrightarrow{c})=(\overrightarrow{a}\circ\overrightarrow{b})+(\overrightarrow{a}\circ\overrightarrow{c})\)
- \((r\cdot\overrightarrow{a})\circ\overrightarrow{b}=r\cdot(\overrightarrow{a}\circ\overrightarrow{b})\)
- \(\overrightarrow{a}\circ\overrightarrow{a}=0\Leftrightarrow\overrightarrow{a}=\overrightarrow{0}\)
- \(\overrightarrow{a}\circ\overrightarrow{a}= (\overrightarrow{a})^2 = a^2 = |a|^2\) (weil jeder Vektor mit sich selbst parallel ist)
Im Gegensatz zum Skalarprodukt ist das Ergebnis des Vektorprodukts (Kreuzprodukt) von zwei Vektoren ein Vektor. Bei der skalaren Multiplikation wiederum multipliziert man nicht zwei Vektoren, sondern einen Skalar und einen Vektor.