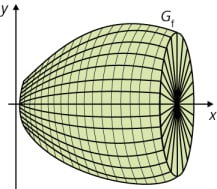
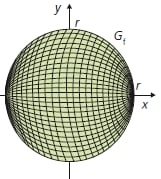
Wenn man ein Kurvenstück einmal um eine Rotationsachse dreht, erhält man die Oberfläche eines Rotationskörpers. Beispielsweise bekommt man einen Zylinder, wenn man eine gerade Strecke um eine dazu parallele Achse dreht, und eine Kugel, wenn das Kurvenstück ein Halbkreis ist die Achse durch dessen Enden läuft (siehe unten).
Das Volumen eines Rotationskörpers lässt sich durch Integration berechnen, wenn das Kurvenstück der Graph Gf einer integrierbaren Funktion f ist und als Rotationsachse die x-Achse eines kartesischen Koordinatensystems gewählt wird. Man betrachtet dabei f bzw. Gf im Intervall [a; b].
Das Volumen des Körpers beträgt dann \(\displaystyle V = \int_a^b\! \pi\cdot (f(x))^2\,\text dx\)
Beispiel:
Halbkreis und Kugel, \(\displaystyle f : x \mapsto \sqrt{r^2-x^2} \ \ ( x \in [- r; r])\)
\(\displaystyle V_\text {Kugel} = \int_{-r}^{r}\! \pi \cdot \left(f(x)\right)^2\,\text dx = \int_{-r}^{r}\! \pi \cdot \left(r^2-x^2\right)\,\text dx = \pi \cdot \left[ r^3 - \frac{x^3}{3} \right]_{-r}^{r} = \frac{4}{3} \pi r^3\)