Der dem griechischen Mathematiker Euklid zugeschriebene Kathetensatz gilt für rechtwinklige Dreiecke und ist Teil der Satzgruppe des Pythagoras. Wenn man die Hypotenuse am Höhenfußpunkt in die beiden Strecken p und q teilt, dann besagt der Kathetensatz, dass jedes Kathetenquadrat so groß ist wie das Rechteck aus Hypotenuse und anliegendem Hypotenusenabschnitt, in Formeln:
a2 = p · c und b2 = q · c
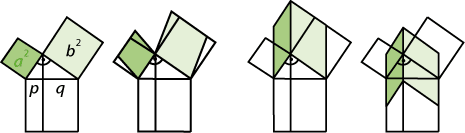
Die Beweisidee illustriert die nachstehende Bilderfolge (man beachte, dass die Fläche eines Parallelogramms gleich bleibt, wenn man eine Seite parallelverschiebt).
Die Umkehrung des Kathensatzes gilt ebenfalls: Wenn bei einem Dreieck hc die Seite c in die Abschnitte p und q teilt und dazu die Beziehungen a2 = p · c und b2 = q · c gelten, dann ist das Dreieck rechtwinklig mit c als Hypotenuse.