In der Geometrie sind Figuren oder Körper einander ähnlich, wenn sie – umgangssprachlich gesprochen – die gleiche Form haben, aber möglicherweise unterschiedlich groß sind. Formal bedeutet Ähnlichkeit, dass man zwei Figuren (Körper) durch eine Ähnlichkeitsabbildung aufeinander abbilden kann. Ähnlichkeitsabbildungen sind alle Kongruenzabbildungen, also Verschiebungen, Drehungen und Spiegelungen, und dazu zentrische Streckungen sowie alle Kombinationen der genannten Abbildungen. Das bedeutet, dass alle kongruenten Figuren (Körper) auch ähnlich, aber nicht alle ähnlichen Objekte auch kongruent sind.
Alle Strecken und Umfänge bei zueinander ähnlichen Figuren bzw. Körpern stehen im selben Verhältnis zueinander (siehe auch Strahlensätze):
\(\displaystyle \frac{a_1}{a_2} = \frac{U_1}{U_2} = k\)
Die Konstante k wird auch Ähnlichkeitsverhältnis genannt.
Flächeninhalte von ähnlichen Figuren verhalten sich zueinander wie die Quadrate von einander entsprechenden Streckenlängen, Rauminhalte (Volumina) wie die Kuben bzw. dritten Potenzen von Streckenverhältnissen:
\(\displaystyle \frac{F_1}{F_2} = k^2; \quad \displaystyle \frac{V_1}{V_2} = k^3\)
Einander entsprechende Winkel sind bei ähnlichen Figuren bzw. Körpern gleich groß.
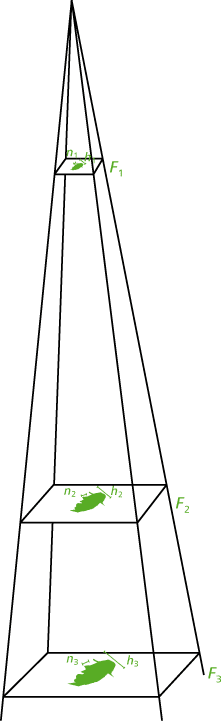
Beispiel:
- Das Ähnlichkeitsverhältnis der Figuren F1 und F2 ist \(\displaystyle \frac{1}{3}\), denn : \(\displaystyle \frac{h_1}{h_2}=\frac{n_1}{n_2}=\frac{1}{3}.\)
- Das Ähnlichkeitsverhältnis der Figuren F3 und F1 ist 4, denn : \(\displaystyle \frac{h_3}{h_1}=\frac{n_3}{n_1}=4.\)
Die Beispiele zeigen: Ist das Ähnlichkeitsverhältnis zweier Figuren F1 und F2 größer als 1, dann ist F1 eine Vergrößerung von F2.
Ist das Ähnlichkeitsverhältnis dagegen eine Zahl zwischen 0 und 1, dann ist F1 eine Verkleinerung von F2.