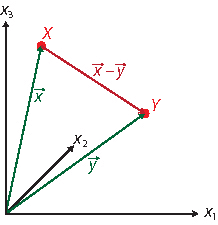Als Differenzvektor oder Verbindungsvektor zweier Punkte X und Y bezeichnet man die Differenz der Ortsvektoren, also den Vektor \(\vec z = \vec x - \vec y\). Der Betrag des Differenzvektors ist der Abstand zwischen den Punkten X und Y.
Anders als Ortsvektoren sind Differenzvektoren unabhängig von der Wahl des Koordinatenursprungs. Würde man den Ursprung z. B. um einen Vektor \(\vec d\) verschieben, würde für die Ortsvektoren von X und Y zwar \(\vec x' = \vec x + \vec d\) und \(\vec y' = \vec y + \vec d\) gelten, der Differenzvektor bliebe aber gleich: \(\vec z' = \vec x' - \vec y' = \vec x + \vec d - \vec y - \vec d = \vec x - \vec y = \vec z\).