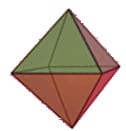
Ein Oktaeder (griech., wörtlich „Achtflächner“) ist ein regelmäßiges Polyeder mit sechs Ecken und ein platonischer Körper. Die acht Seitenflächen eines Oktaeders sind kongruente gleichseitige Dreiecke. Man kann ein Oktaeder auch als zwei an ihren quadratischen Grundflächen zusammengeklebte, identische Pyramiden auffassen.
Das Volumen eines Oktaeders mit der Seitenlänge a beträgt \(\displaystyle V = \frac{\sqrt 2}{3}a^3\), der Oberflächeninhalt \(\displaystyle A = 2\sqrt 3\cdot a^2\).
Das Oktaeder hat zahlreiche Dreh- und Spiegelsymmetrien und ist punktsymmetrisch bezüglich seines Mittelpunkts (Symmetrie).
Wenn man die Seitenmitten eines Oktaeders verbindet, erhält man einen Würfel (und umgekehrt).