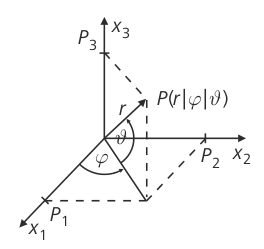
Statt durch kartesische Koordinaten kann die Lage eines Punkts im Koordinatensystem auch durch Kugelkoordinaten angegeben werden. Deren Komponenten sind der Abstand r vom Ursprung und zwei Winkel auf der Oberfläche der Einheitskugel, die im Wesentlichen den aus der Geografie bekannten Längen- und Breitengraden entsprechen: Der Winkel \(\varphi\) (der „Längenwinkel“) läuft dabei von 0° bis 360° (im Bogenmaß von 0 bis \(2\pi\)) einmal um den Äquator, der Winkel \(\vartheta\) (der „Breitenwinkel“) von –90° bis +90° (im Bogenmaß von \(\displaystyle -\!\frac{\pi}{2}\) bis \(\displaystyle +\!\frac{\pi}{2}\)) vom Südpol zum Nordpol.
Für die kartesischen Koordinaten des Punkts P(P1|P2|P3) gilt:
\(P_1 = r \cdot \cos \vartheta \cdot \cos \varphi\)
\(P_2 = r \cdot \cos \vartheta \cdot \sin \varphi\)
\(P_3 = r \cdot \sin \vartheta\)
Das zweidimensionale Gegenstück zu den Kugelkoordinaten sind die Polarkoordinaten.