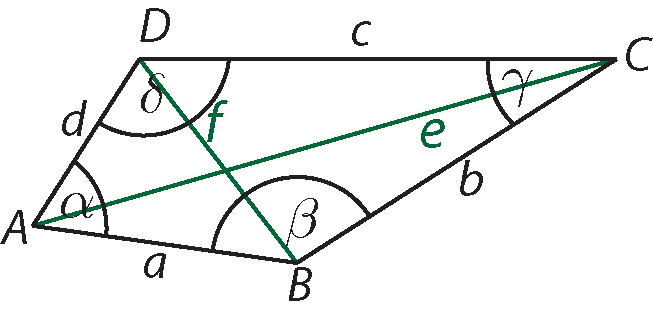
Eine Diagonale verbindet zwei nicht benachbarte Punkte in einem Viereck. oder einem Polygon (Vieleck). Im Viereck heißt die Diagonale zwischen den Punkten A und C gewöhnlich e, die zwischen B und D nennt man f.
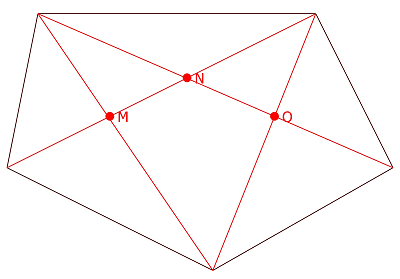
Punkte, in denen sich Diagonalen schneiden, nennt man Diagonalenschnittpunkte. In einem Polygon mit mehr als vier Ecken kann es mehrere Diagonalenschnitpunkte geben.
In einem Rechteck oder Quadrat (das natürlich auch ein Rechteck ist) sind beide Diagonalen gleich lang und man kann ihre Länge mit dem Satz des Pythagoras ausrechenen: \(d = (e = f =) \sqrt{ a^2 + b^2}\). Im Quadrat gilt \(d = a \cdot \sqrt 2\).
In Körpern, insbesondere in Polyedern wie etwa einem Quader, muss man zwischen den Flächendiagonalen auf Oberflächen bzw. Schnittflächen und der Raumdiagonalen unterscheiden. Eine Raumdiagonale verbindet Punkte, zwischen denen drei und nicht zwei Kanten liegen (Abbildung).
Für die Raumdiagonale im Quader mit Seitenlängen a, b und c erhält man mit zweimaligem Anwenden des Pythagoras-Satzes: \(d = \sqrt{ a^2 + b^2 + c^2}\). Im Würfel ist \(d = a \cdot \sqrt 3\).