Eine Zahlenfolge, bei der die Differenz d = an+1 – an von zwei aufeinanderfolgenden Gliedern für alle n∈N gleich groß (konstant) ist, nennt man einen arithmetische Zahlenfolge.
Die Bezeichnung „arithmetische Zahlenfolge“ kommt daher, dass von drei aufeinanderfolgenden Gliedern an–1, an und an+1 das mittlere Glied an immer gleich dem arithmetischen Mittel der beiden äußeren Glieder ist: an=an−1+an+12 (n∈N).
Für arithmetische Zahlenfolgen gilt das explizite Bildungsgesetz: an = a1 + (n – 1) · d (n∈N).
Beispiel:
- Die Zahlenfolge (an) = –1; 0,5; 2; 3,5; 5; … hat das explizite Bildungsgesetz an = –1 + (n – 1) · 1,5 (n∈N), also d = 1,5.
Wenn die Differenz d zweier benachbarter Folgenglieder positiv ist (d > 0), nimmt die Zahlenfolge streng monoton zu, bei d = 0 ist sie konstant und für d < 0 nimmt sie streng monoton ab.
Die Punkte Pn(n|an), die den Funktionsgraphen einer arithmetischen Zahlenfolge liegen auf der Geraden mit der Gleichung y = f(x) = d · x + (a1 – d), und zwar immer bei ganzzahlig-positiven x-Werten.
Beispiele:
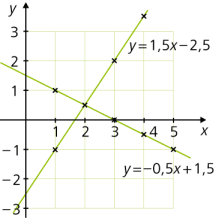
- an=−1+(n−1)⋅1,5: y=1,5x+(−1−1,5)=1,5x−2,5
- an=1+(n−1)⋅(−0,5): y=−0,5x+(1−(−0,5))=−0,5x+1,5
p>