Abbildungsmatrizen

In der Analytischen Geometrie versteht man unter einer Abbildungsmatrix eine Matrix, die eine lineare Abbildung (Drehung, Verschiebung, Spiegelung) zwischen Vektoren beschreibt.

• Eine lineare Abbildung f zwischen zwei Vektoren \(\overrightarrow{x}\) und \(\overrightarrow{x}'\) (bzw. zwischen zwei Vektormengen bzw. Vektorräumen X und \(X'\)) kann man formal wie eine proportionale Zuordnung bzw. Funktion zwischen normalen Zahlen schreiben:
  \(f: X \longrightarrow X', \ \overrightarrow{x} ' = f(\overrightarrow{x}) = A \cdot \overrightarrow{x} \)
  Dabei sind \(\overrightarrow{x} \in X\) der Urbildvektor bzw. -punkt (sozusagen die unabhängige Variable), \(\overrightarrow{x}' \in X'\) der Bildvektor bzw. -punkt (die abhängige Variable) und A die Abbildungsmatrix.
   
• Wenn außerdem noch ein Verschiebungsvektor \(\overrightarrow{v}\) als konstanter Summand addiert wird, handelt es sich um eine affine Abbildung (zentrische Streckungen oder Scherungen sind affine Abbildungen, die nicht linear sind):
  \(\tilde f: X \longrightarrow X', \ \overrightarrow{x} ' = \tilde f(\overrightarrow{x}) = A \cdot \overrightarrow{x} + \overrightarrow{v}\)

Die Abbildungsmatrix A entspricht also in der Vektorgleichung der Steigung m einer sog. linearen Funktion und der Verschiebungsvektor dem y-Achsenabschnitt b. Wegen dieser Entsprechungen nennt man die Analytische Geometrie auch „Lineare Algebra“.

Achtung: Es gibt hier etwas unterschiedliche Sprechweisen – in der Geometrie heißt die Abbildung ohne Verschiebungsvektor (\(f(\overrightarrow{x}) = A \cdot \overrightarrow{x} \)) „linear“ und die mit Verschiebungsvektor (\(\tilde f(\overrightarrow{x}) = A \cdot \overrightarrow{x} + \overrightarrow{v}\)) „affin“, in der Analysis spricht man ohne y-Achsenabschnitt (f(x) = mx) von einer „proportionalen“ und mit y-Achsenabschnitt ((f(x) = mx + b) von einer „linearen“ Funktion.

In Komponentenschreibweise lautet die Abbildungsgleichung bei einer 2×2-Matrix

\(\begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} \\ a_{11} & a_{12} \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2\end{pmatrix} + \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}\)

Man muss also den Vektor \(\overrightarrow{x}\) von links mit der Matrix A multiplizieren und dann den konstanten Vektor \(\overrightarrow{v}\) addieren. Natürlich lassen sich entsprechende Gleichungen auch im dreidimensionalen Raum aufstellen, die Vektoren haben dann drei Einträge und die Abbildungsmatrix neun.

Die Abbildungsmatrizen von Drehungen und Spiegelungen (Dreh- und Spiegelmatrizen) sind Orthogonalmatrizen, d. h., sie haben die Determinante \(\pm 1\) und ihre Transponierte ist gleich ihrer inversen Matrix: A^T = A^–1 bzw. A^TA = AA^T = 1.

Es spricht nichts dagegen, auch vierdimensionale oder noch größere Matrizen und Vektoren zu betrachten. Wenn man sich mit Vektoren beschäftigt, die mehr als zwei oder drei Komponenten haben, muss man beachten, dass dieselbe Abbildung durch Matrizen mit unterschiedlichen Komponenten dargestellt wird, sofern man verschiedene Basen für die Vektorräume X und \(X'\) wählt werden (auch Vektoren sehen anders aus, wenn man den Koordinatenursprung verschiebt). Die Abbildungsmatrix muss auch nicht unbedingt quadratisch sein, sie muss nur genauso viele Zeilen haben wie \(\overrightarrow{x}\) Komponenten hat und so viele Spalten wie \(\overrightarrow{x}'\) Komponenten hat.

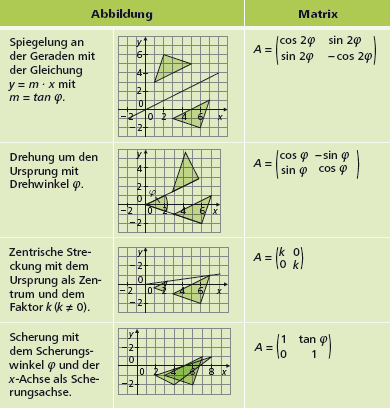
Beispiele:

Die ersten beiden der folgenden Beispiele beschreiben lineare, die beiden anderen nichtlineare affine Abbildungen in der (zweidimensionalen) Ebene.