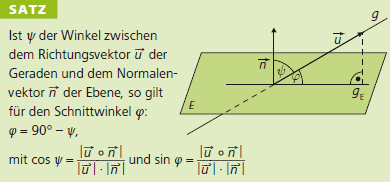
Unter dem Schnittwinkel \(\varphi\) zwischen einer Geraden g und einer Ebene E versteht man den nicht stumpfen Winkel zwischen dem Normalenvektor \(\vec n\) der Ebene der senkrechten Projektion gE des Richtungsvektors \(\vec u\) der Geraden auf die Ebene. Dies ist also nicht der Winkel \(\psi\) zwischen \(\vec n\) und \(\vec u\), sondern es gilt \(\varphi = 90^\circ - \psi\) (siehe Abbildung).
Dabei sind \(g : \overrightarrow{x} = \overrightarrow{a} + \lambda \cdot \overrightarrow{u} (\lambda \in \mathbb{R})\) und \(E: \overrightarrow{n} \circ ( \overrightarrow{x} - \overrightarrow{a} ) = 0\) (mit dem Stützvektor bzw. Aufpunkt \(\vec a\)) und „\(\circ\)“ bezeichnet das Skalarprodukt zwischen \(\vec u\) und \(\vec n\).
Achtung: Wenn die Ebenengleichung nicht in Normalenform vorliegt, muss man sie zunächst entsprechend umwandeln.
Beispiel:
\(g : \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} -2 \\ 7 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix} , \lambda \in \mathbb{R};\) \(E: 2 x_1 - 6 x_2 + 3 x_3 + 4 = 0\)
\(\displaystyle \sin \varphi = \frac{\left| \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 2 \\ -6 \\ 3 \end{pmatrix} \right|}{\sqrt{ 3^2 + 2^2 + 1^2} \cdot \sqrt{2^2 + (-6)^2 + 3^2}} = \frac{3}{\sqrt{14 \cdot 49}}\)
\(\displaystyle \varphi = \sin^{-1}\frac{3}{7 \cdot \sqrt{14}} \approx 6,6^{\circ}\)
Den Schnittwinkel zwischen zwei Geraden bzw. zwischen zwei Ebenen bestimmt man ganz ähnlich.