Unter dem Schnittwinkel zweier Funktionsgraphen \(G_{f_1}\) und \(G_{f_2}\) an einer Stelle x0 versteht man den nichtstumpfen Winkel \(\varphi\), unter dem sich die Tangenten an die beiden Graphen in diesem Punkt schneiden. Für diesen Winkel gilt
\(\displaystyle \tan \varphi = \left| \frac{m_1 - m_2}{1 + m_1 \cdot m_2} \right| = \left| \frac{f_1'(x_0) - f_2'(x_0)}{1 + f_1'(x_0) \cdot f_2'(x_0)} \right|\)
Im Spezialfall, dass die Graphen senkrecht aufeinander stehen, so gilt: \(f_1 ' ( x_0 ) \cdot f_2 ' ( x_0 ) = m_1 \cdot m_2 = - 1\).
Beispiel:
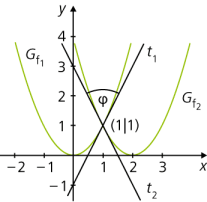
Die Graphen der Funktionen \(f_1\!: x \mapsto x^2\) und \(f_2\! : x \mapsto (x - 2)^2\) schneiden sich an der Stelle x0 = 1.
Mit \(m_1 = f_1 ' ( x_0 ) = 2 x_0 = 2\) und \(m_2 = f_2 ' ( x_0 ) = 2 x_0 - 4 = - 2\) ergibt sich
\(\tan \varphi = \left| \dfrac{2-(-2)}{1+2\cdot (-2)} \right| = \dfrac{4}{3} \ \ \Rightarrow \ \ \varphi \approx 53^\circ\)
Die Tangenten im Schnittpunkt (1|1) sind
\(t_1\! :\ y = 2x - 1\) und \(t_2\! :\ y = - 2x + 3\).