Die Binomialverteilung ist die wichtigste (diskrete) Wahrscheinlichkeitsverteilung. Sie gibt die Wahrscheinlichkeit dafür an, in einer Bernoulli-Kette eine bestimmte Anzahl von „Erfolgen“ zu erzielen. Wenn die beiden möglichen Ausgänge des Einzelexperiments die Wahrscheinlichkeit p („Erfolg“) und 1 – p („verloren“) haben, dann beträgt die Wahrscheinlichkeit, bei n Wiederholungen genau k-mal Erfolg zu haben,
P(X=k) = B_{n; p}(k)= \begin{pmatrix}n\\k\end{pmatrix} \cdot p^k \cdot (1-p)^{n-k}
dabei sind n \in \mathbb{N}, 0 \le p \le 1 , k \in \{0; 1; \ldots n\} und X ist die Zufallsvariable, die beschreibt, wie oft bei n Versuchen „Erfolg“ herauskommt. Der Ausdruck \begin{pmatrix}n\\k\end{pmatrix} heißt Binomialkoeffizient. Die Wahrscheinlichkeit, höchstens bzw. mindestens k-mal „Erfolg“ zu haben, berechnet man mit der kumulierten Binomialverteilung.
Beispiel:
Eine (faire) Münze wird 12-mal geworfen. Dann beträgt die Wahrscheinlichkeit, genau 8-mal „Zahl“ zu bekommen, B_{12; \ 0,5}(8)= \begin{pmatrix}12\\8\end{pmatrix} \cdot 0,5^8 \cdot (1-0,5)^{12-8} \approx 12,1\, \%.
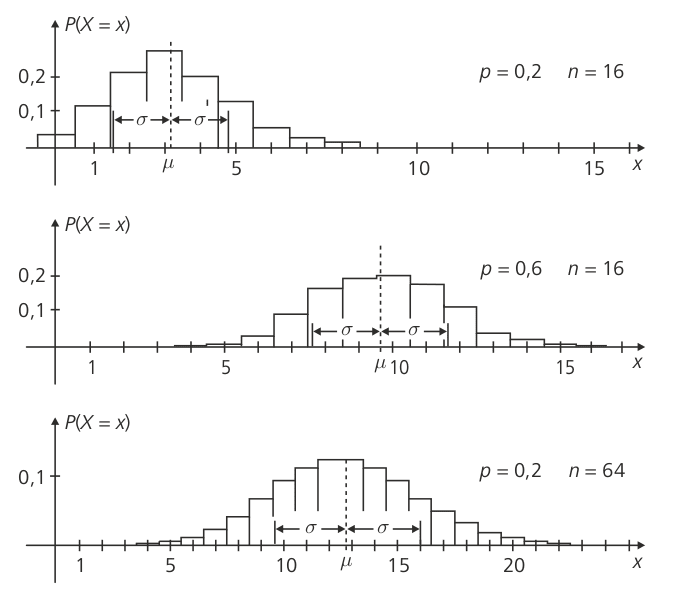
Der Erwartungswert E(X) = \mu einer binomialverteilten Zufallsvariablen X beträgt n \cdot p, für die Varianz gilt \text{Var}(X) = \sigma^2=n \cdot p \cdot (1-p).
Wenn der Einzelversuch der Bernoulli-Kette sehr oft durchgeführt wird und p nicht zu klein ist, kann man die Binomialverteilung durch die Normalverteilung annähern. Als Faustregel kann man sagen, dass diese Näherung erlaubt ist, wenn \sigma^2=n \cdot p \cdot (1-p) \ge 9 und/oder \mu =n \cdot p \ge 4 ist.
Beispiele für binomialverteilte Zufallsgrößen mit unterschiedlichen Werten für die Parameter p und n: