Was du wissen musst
-
Was ist der absolute Betrag?
Der absolute Betrag ist das Gleiche wie der Betrag. Es handelt sich dabei also nur um ein Synonym. Es ist möglich, dass du statt der Schreibweise mit den Betragsstrichen \(|x|\) auch die Schreibweise \(\text{abs}(x)\) zu sehen bekommst. Dabei handelt es sich aber nur um eine andere Schreibweise für den Betrag und diese hat sonst keinen weiteren Einfluss auf deine Rechnungen.
-
Wie bestimmt man den Betrag einer Zahl?
Der Betrag einer Zahl gibt immer ihren Abstand zur Zahl Null an. Der Betrag ist also immer positiv.
Um beispielsweise den Betrag von \(4\) zu bestimmen, musst du dir überlegen, wie weit die Zahl \(4\) auf dem Zahlenstrahl von der Zahl \(0\) entfernt ist.
\(|4|=4 \)
Das gilt auch, wenn du den Betrag der Zahl \(-4\) bestimmen möchtest. Stell dir den Zahlenstrahl vor und du wirst feststellen, dass die Zahl \(-4\) den gleichen Betrag wie die Zahl \(4\) hat, denn beide haben den gleichen Abstand zu \(0\).
\(|-4|=4 \)
-
Wie löst man Gleichungen mit Betrag?
Um eine Betragsgleichung durch Fallunterscheidung zu lösen, musst du folgende Schritte abarbeiten:
1. Durch eine Fallunterscheidung in zwei Fälle kannst du den Betrag auflösen. In einem Fall ist der Term im Betrag positiv. Dann kannst du den Term einfach ohne die Betragsstriche schreiben. Im anderen Fall ist der Term im Betrag kleiner als \(0\). Dann musst du die Betragsstriche weglassen und die Vorzeichen des gesamten Terms ändern:
Beispiel: \(|x-1|+2=6\)
Wir betrachten zunächst nur den Term zwischen den Betragsstrichen. Du untersuchst, wann \(x\) größer oder gleich \(0\) ist:
\(\begin{align*} x-1&\geq 0&&\mid+1\\ x&\geq1 \end{align*} \)
Im Abschnitt \(x\geq1\) ist der Inhalt des Betrags größer oder gleich \(0\). Der Term kann also unverändert bleiben. Der zweite Fall beinhaltet dann alle anderen Zahlen, also \(x<1\). Für diese Zahlen ist der Inhalt des Betrags negativ. Die Vorzeichen des Terms müssen für diesen Fall also geändert werden.
Daraus ergibt sich:
\(|x-1| = \begin{cases} x-1 &\text{für } x \geq 1\\ -x+1 &\text{für } x < 1 \end{cases}\)
Wenn du das in die Ausgangsgleichung einsetzt, erhältst du:
Fall 1: \(x-1+2=6\)
Fall 2: \(-x+1+2=6\)
2. Als Nächstes musst du die Lösungsmenge der einzelnen Fälle bestimmen. Das bedeutet, dass du die entstandenen Gleichungen auflösen musst:
Für den 1. Fall \((x \geq 1)\) ergibt sich folgende Gleichung, die nach \(x\) aufgelöst werden muss:
\(\begin{align*} x-1+2&=6\\ x+1&=6&&\mid-1\\ x&=5 \end{align*}\)
\(\mathbb{L}_1=\{5\}\)
Für den 2. Fall \((x<1)\) ergibt sich folgende Gleichung, die nach \(x\) aufgelöst werden muss:
\(\begin{align*} -x+1+2&=6\\ -x+3&=6&&\mid-3\\ -x&=3&&\mid:(-1)\\ x&=-3 \end{align*}\)
\(\mathbb{L}_2=\{-3\}\)
3. Zum Schluss musst du nur noch die Lösungsmenge der gesamten Betragsgleichung aufschreiben:
\(\mathbb{L} =\mathbb{L}_1\cup\mathbb{L}_2=\{5\}\cup\{-3\}=\{5;-3\}\)
Es ist auch möglich, eine Betragsgleichung durch Quadrieren zu lösen. Durch das Quadrieren verschwindet der Betrag, denn es gilt: \(|x|^2 = x^2\). Du erhältst eine quadratische Funktion, die du in ihre allgemeine Form bringen und dann mithilfe der p-q-Formel lösen kannst.
-
Wie löst man Ungleichungen mit Betrag?
Um eine Ungleichung mit Betrag durch Fallunterscheidung zu lösen, kannst du die gleiche Vorgehensweise wie bei Gleichungen mit Betrag nutzen. Nur ein paar Besonderheiten musst du beachten:
1. Durch eine Fallunterscheidung in zwei Fälle kannst du den Betrag auflösen. In einem Fall ist der Term im Betrag positiv. Dann kannst du den Term einfach ohne die Betragsstriche schreiben. Im anderen Fall ist der Term im Betrag kleiner als \(0\). Dann musst du die Betragsstriche weglassen und die Vorzeichen des gesamten Terms ändern:
Beispiel: \(|x+3|+2<3\)
Wir betrachten zunächst nur den Term zwischen den Betragsstrichen. Du untersuchst, wann \(x\) größer oder gleich \(0\) ist:
\(\begin{align*} x+3&\geq 0&&\mid-3\\ x&\geq-3 \end{align*} \)
Daraus ergibt sich:
\(|x+3| = \begin{cases} x+3 &\text{für } x \geq -3\\ -x-3 &\text{für } x < -3 \end{cases}\)
Wenn du das in die Ausgangsgleichung einsetzt, erhältst du:
Fall 1: \(x+3+2<3\)
Fall 2: \(-x-3+2<3\)
2. Als Nächstes musst du die Lösungsmenge der einzelnen Fälle bestimmen. Das bedeutet, dass du die entstandenen Ungleichungen auflösen musst. Denk daran, dass du hier eine Ungleichung umstellst und besondere Regeln gelten. Die Lösungsmenge einer Ungleichung ergibt sich, wenn du die Bedingung mit dem Ergebnis abgleichst und dir überlegst, an welcher Stelle sie sich überschneiden:
Für den 1. Fall \((x \geq -3)\) ergibt sich folgende Gleichung, die nach \(x\) aufgelöst werden muss:
\(\begin{align*} x+3+2&<3\\ x+5&<3&&\mid-5\\ x&<-2 \end{align*}\)
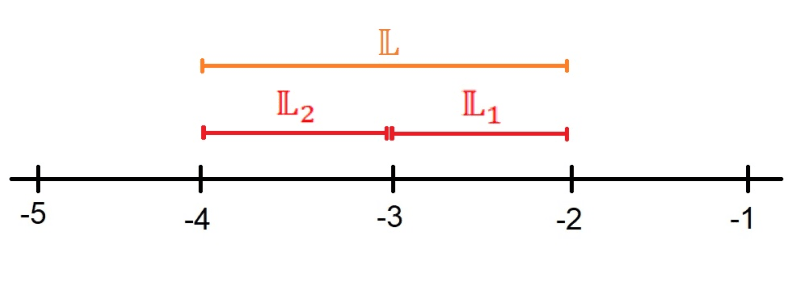
Durch das Übereinanderlegen der Bedingung \(x \geq -3\) und des Ergebnisterms \(x<-2\) ergibt sich folgende Lösungsmenge:
\(\mathbb{L}_1=\{-3\leq x<-2\}\)
Für den 2. Fall \((x<-3)\) ergibt sich folgende Gleichung, die nach \(x\) aufgelöst werden muss:
\(\begin{align*} -x-3+2&<3\\ -x-1&<3&&\mid+1\\ -x&<4&&\mid:(-1)\\ x&>-4 \end{align*}\)
Durch das Übereinanderlegen der Bedingung \(x < -3\) und des Ergebnisterms \(x>-4\) ergibt sich folgende Lösungsmenge:
\(\mathbb{L}_2=\{-4<x<-3\}\)
3. Zum Schluss musst du nur noch die Lösungsmenge der gesamten Betragsgleichung aufschreiben:
\(\begin{align*} \mathbb{L} &=\mathbb{L}_1\cup\mathbb{L}_2\\ \mathbb{L} &=\{-3\leq x<-2\}\cup\{-4<x<-3\}\\ \mathbb{L}&=\{-4<x<-2\} \end{align*}\)
Alternativ kannst du Ungleichungen mit Betrag auch durch Quadrieren lösen.
-
Was ist die Betragsfunktion?
Eine Betragsfunktion ist eine Funktion, die aus zwei unterschiedlich definierten Abschnitten zusammengesetzt ist. Ihre Funktionsgleichung lautet:
\(f(x)=|x| \)
\(|x| = \begin{cases} x &\text{für } x \geq 0\\ -x &\text{für } x < 0 \end{cases}\)
Das sieht viel komplizierter aus, als es tatsächlich ist. Es bedeutet nur, dass der Wert für alle positiven Zahlen, also alle Zahlen größer \(0\), unverändert bleibt und für alle negativen Zahlen ein Minus vor das Argument geschrieben wird, wodurch sie positiv werden. Du kannst also die ursprünglichen Werte an der y-Achse spiegeln. Das ergibt für die Funktion \(f(x)=|x| \) einen Funktionsgraphen, der aus zwei linearen Funktionen zusammengesetzt ist.