Was ist eine Äquivalenzumformung?

Äquivalenzumformungen werden in der Schule sehr häufig verwendet. Da sie nicht an ein bestimmtes Themengebiet geknüpft sind und von der 7. Klasse bis zum Abitur oder Studium benötigt werden, ist es ganz besonders wichtig, dass du sie sicher beherrschst.

Eine Äquivalenzumformung ist das Umformen einer Gleichung, bei der die Beziehung erhalten bleibt. Erlaubt sind also nur Operationen, durch die die Aussage \(\text{linke Seite} = \text{rechte Seite}\) weiterhin richtig ist.

Dafür findest du hier nicht nur Erklärungen, was genau Äquivalenzumformungen sind, wie du bei Äquivalenzumformungen mit Wurzeln umgehen und was du bei Ungleichungen beachten musst, sondern selbstverständlich auch viele interaktive Übungen, die dein Verständnis fördern und deine Fähigkeiten trainieren sollen, und Klassenarbeiten zur Vorbereitung auf deine Prüfungen.

Was sind Äquivalenzumformungen?

Video wird geladen...

Äquivalenzumformung

Was du wissen musst

  • Wie wendet man Äquivalenzumformungen an?

    Bei Äquivalenzumformungen musst du immer einen Grundsatz beachten:

    Alle Operationen müssen auf beiden Seiten des Gleichheitszeichens ausgeführt werden.

     

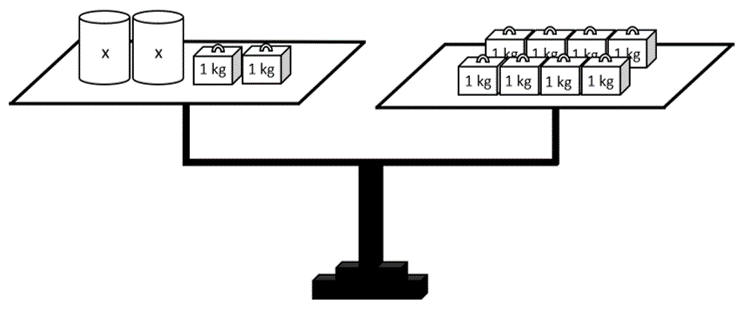
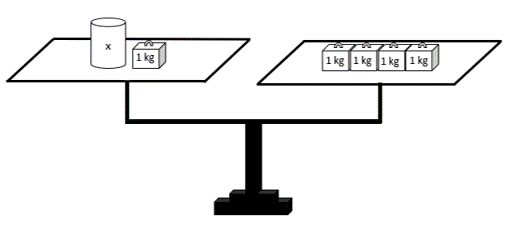
    Du kannst dir dafür vorstellen, die Gleichung wäre eine Waage. Beide Seiten sind gleich, also befindet sich die Waage im Gleichgewicht. Wenn du jetzt auf einer Seite etwas hinzufügst, dann musst du dies auch auf der anderen Seite tun, sonst ist die eine Seite der Gleichung größer bzw. die eine Seite der Waage schwerer.
    Das Gleiche gilt, wenn du etwas wegnimmst, beide Seiten verdoppelst, halbierst und so weiter.

    Wenn du eine Äquivalenzumformung benutzen willst, solltest du das kenntlich machen. Das tust du, indem du einen senkrechten Strich hinter deine Gleichung machst. Dahinter schreibst du dann die Operation, die du durchführen willst. In der nächsten Zeile wendest du sie dann auf beiden Seiten der Gleichung an.

    Auch wenn dich eine Äquivalenzumformung nicht näher ans Ziel bringt, ist sie nicht falsch. Wenn du keine Rechenfehler machst, bleibt die Gleichung immer erhalten, auch wenn sie umgeformt wird.

    Beispiel:

    Eine Gleichung ist als Bild mit Gewichten vereinfacht worden.

    \(\begin{align} 2 \cdot x + 2 &= 8 \qquad |:2 \\ \left( 2 \cdot x + 2 \right) :2 &= 8 :2 \\ x + 1 &= 4 \end{align}\)

    Äquivalene Termumformung in Waagenoptik (nach der Umformung)

     

  • Welche Arten von Äquivalenzumformungen gibt es?

    Am häufigsten benutzt man die vier Grundrechenarten:

    • Addition
    • Subtraktion
    • Multiplikation
    • Division

    Manchmal wird auch quadriert, ein anderer Exponent benutzt oder eine Wurzel gezogen. Dabei musst du allerdings aufpassen, da du beim Wurzelziehen etwas beachten musst.

    Für alle Rechenarten gilt immer, dass du alle Operationen auf beiden Seiten der Gleichung durchführen musst. Wenn du diesen Grundsatz beachtest und aufpasst, dass du dich nicht verrechnest, kann eigentlich nicht mehr viel schiefgehen.

  • Welche Besonderheiten muss man beim Wurzelziehen beachten?

    Beim Ziehen von Wurzeln muss man etwas vorsichtiger sein als bei den anderen Operationen. Sonst kann es dazu kommen, dass man „Lösungen verliert“. Das kann man sich an einem ganz einfachen Beispiel überlegen:

    Es gibt zwei Möglichkeiten, mit einem Quadrat auf die Zahl \(4\) zu kommen: Man quadriert \(+2\) oder \(-2\).

    Zieht man die Wurzel aus \(4\), erhält man als Ergebnis nur die positive Zahl, also \(+2\).

    \(\left( +2 \right)^2 = 4\) und \(\left( -2 \right)^2 = 4\)
     

    \( \begin{align} x^2&=4 \quad | \sqrt{(\dots)}\\ x &=2 \end{align}\)

    Irgendwo in der Rechnung „verschwindet“ die negative Lösung (\(-2\)). Das passiert in dem Moment, in dem die Wurzel gezogen wird. Da Wurzeln nur aus positiven Zahlen gezogen werden dürfen, ergibt sich aus der Rechnung auch nur die positive Lösung. Trotzdem weißt du ja bereits, dass Quadrate immer zwei Basen haben können, die jeweils den gleichen Betrag, aber unterschiedliche Vorzeichen haben.

    Deshalb musst du immer, wenn du mit einer Wurzel eine Lösung ausrechnest, an der Wurzel dazuschreiben, dass du die positive und die negative Möglichkeit betrachtest (\(\pm\)), und im weiteren Verlauf mit zwei Lösungen rechnen (\(x_1\) und \(x_2\)).

    Wenn man verschiedene Lösungen betrachtet, nennt man das eine Fallunterscheidung.

    \( x^2=4 \quad | \color{red}{\pm}\sqrt{(\dots)}\)
    \(x_1=2\) oder \(\color{red}{x_2=-2}\)

    Aber weiterhin gilt: Aus negativen Zahlen darfst du keine Wurzeln ziehen.

  • Wie funktionieren Äquivalenzumformungen bei Ungleichungen?

    Auch bei Ungleichungen kannst du Äquivalenzumformungen wie gewohnt anwenden. Auch hier gilt, dass alle Operationen auf beiden Seiten vollzogen werden müssen. Allerdings kann es dazu kommen, dass sich die Relation zwischen den beiden Seiten umdreht.

    Das bedeutet, aus größer als wird kleiner als (oder umgekehrt) oder aus größer gleich wird kleiner gleich (bzw. andersherum).

    \(x_1 > y_1 \quad \)wird zu \(\quad x_2<y_2\)
    \(x_1\geq y_1 \quad \)wird zu\(\quad x_2 \leq y_2\)

    Dies passiert immer, wenn du:

    • mit einer negativen Zahl multiplizierst
    • durch eine negative Zahl dividierst
    • du potenzierst (zum Beispiel quadrierst) und beide Seiten negativ sind
    • du potenzierst, eine Seite positiv und die andere negativ ist, aber die negative Seite vom Betrag her größer ist.

    Auch beim Wurzelziehen gibt es etwas zu beachten. Bei der positiven Lösung bleibt die Ungleichung erhalten, aber

    • bei der negativen Lösung beim Wurzelziehen

    dreht sich die Relation auch um.

Zugehörige Klassenarbeiten