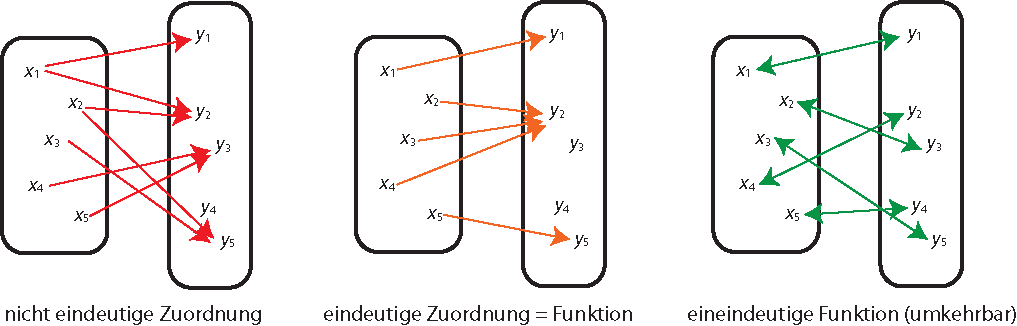
Eine mathematische Zuordnung (Relation) oder Abbildung heißt eindeutig, wenn jedem Element der Definitionsmenge bzw. des Urbilds X höchstens ein Element der Wertemenge (Zielmenge) bzw. des Abbilds Y zugewiesen wird. Anders ausgedrückt: Kein \(x \in X\) wird zwei (oder mehr) verschiedenen Elementen aus Y zugeordnet.
Eine eindeutige Zuordnung nennt man eine Funktion. Eine Funktion hat also nie zwei verschiedene Funktionswerte zum selben x – darum kann ein Vollkreis nicht der Graph einer Funktion sein, denn dort würden fast jedem x innerhalb des Definitionsbereichs ein oberer und ein unterer Wert zugeordnet.
Achtung: Manchmal wird das Wort „Zuordnung“ auch als ein Synonym von „Funktion“ benutzt.
Bei einer eineindeutigen Zuordnung bzw. Abbildung hat auch jedes Element des Abbilds Y nur ein Element des Urbilds X, das ihm zugeordnet wird. Zu jedem \(x \in X\) gehört genau ein \(y \in Y\) und zu jedem \(y \in Y\) genau ein \(x \in X\). Jede eineindeutige Zuordnung ist auch eindeutig, also eine Funktion. Eineindeutige Funktionen sind umkehrbar. Ein anderer Name für eineindeutig ist bijektiv.