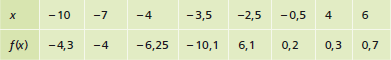Betrachtet wird die Funktion \(f : x \mapsto \frac{x^3 - x^2 - x + 1}{4 x^2 + 16x + 12} = \frac{u (x)}{v (x)}\) .
Bestimmung der Nullstellen von Nenner und Zähler
Nenner: \(v (x) = 4 x^2 + 16x + 12 = 0 \Leftrightarrow x = - 3\) oder \(x = - 1\)
Damit erhält man: \(D_f = \mathbb{R}\backslash\{- 3; - 1\}\).
Zähler: \(u (x) = x^3 - x^2 - x + 1 = 0 \Leftrightarrow u(x) = (x - 1)^2 \cdot (x + 1) \Leftrightarrow x = - 1\) oder \(x = 1\) (doppelte Nullstelle von \(u\)),
\(x = 1\) ist (doppelte) Nullstelle von \(f\), da \(u (1) = 0\) und \(v (1) \neq 0\).
\(x = - 1 \notin D_f\) , also keine Nullstelle von \(f\).
Vereinfachen von \(f (x)\)
Da \(x = - 1\) gemeinsame Nullstelle des Zählers und des Nenners ist, kann der Term \((x + 1)\) gekürzt werden. Für \(x \in \mathbb{R}\backslash\{- 3; - 1\}\) ist \(f (x) = \frac{x^3 - x^2 - x + 1}{4 x^2 + 16x + 12} = \frac{(x - 1 )^2 (x + 1)}{4(x + 3)(x + 1)} = \frac{(x - 1 )^2}{4(x + 3)}\) .
Verhalten an den Definitionslücken
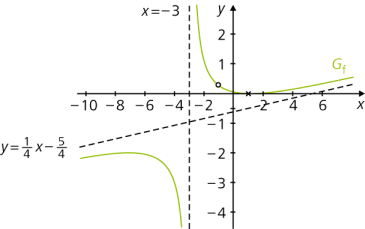
Lücke \(x = - 3\): (Einfache) Polstelle, da \(x = - 3\) (einfache) Nullstelle des Nenners, jedoch keine Nullstelle des Zählers \((x - 1 )^2\) ist.
Verhalten an der Polstelle:
\(\lim\limits_{\underset{x<-3}{x \to {-3}}}f(x)=-\infty\) und \(\lim\limits_{\underset{x>-3}{x \to {-3}}}f(x)=+\infty\)
Lücke \(x = - 1\): Stetig hebbare Definitionslücke, da \(\lim\limits_{\underset{x<-1}{x \to {-1}}}f(x)=\lim\limits_{\underset{x>-1}{x \to {-1}}}f(x)=+0,5\)
Bei \(x = - 1\) hat der Graph \(G_f\) eine Lücke.
Bestimmung der Asymptoten
Vertikale Asymptote \(x = - 3\) (Polstelle)
Die schräge Asymptote erhält man durch Polynomdivision:
\((x - 1 )^2 : [4 (x + 3)] = ( x^2 - 2x + 1) : (4x + 12) = \frac{1}{4} x - \frac{5}{4} + \frac{16}{4x+12}\) .
Es gilt also für \(f : f (x) = \frac{1}{4} x - \frac{5}{4} + \frac{16}{4x+12} = g (x) + r (x)\) mit \(g (x) = \frac{1}{4} x - \frac{5}{4}\) und \(r (x) = \frac{16}{4x+12}\) .
Wegen \(\lim\limits_{x \to \pm \infty}[ f (x) - g (x) ] = \lim\limits_{x \to \pm \infty} [ r (x) ] = \lim\limits_{x \to \pm \infty} \frac{16}{4x+12} = 0\) ist die Gerade \(g : y = \frac{1}{4} x - \frac{5}{4}\) schräge Asymptote von \(G_f\) .
Berechnung weiterer Funktionswerte
Wertetabelle:
Zeichnung des Graphen unter Verwendung der bisherigen Ergebnisse
Genauere Untersuchungen können in einer Kurvendiskussion (s. Diskussion einer gebrochenrationalen Funktion - Anwendungsbeispiele) erfolgen.