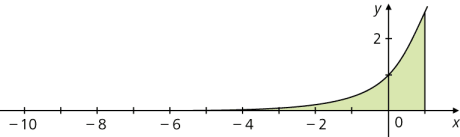Der Begriff des uneigentlichen Integrals erweitert das bestimmte Integral auf solche Fälle, in denen der Integrand f(x) divergent ist oder der Integrationsbereich sich ins Unendliche erstreckt. Man betrachtet in solchen Fällen den Grenzwert der Integralfunktion – wenn dieser existiert, nennt man ihn ein uneigentliches Integral Iu und schreibt z. B.:
\(I_{\text u} = \displaystyle \int\limits_{a}^{\infty} f(x)\, \text dx = \lim_{b \to \infty}\textstyle \int\limits_{a}^{b} f(x)\, \text dx = \displaystyle \lim_{b \to \infty} \left[ F(x) \right]^b_1 = \lim_{b \to \infty} \left[ F(b) - F(a) \right]\)
Beispiele:
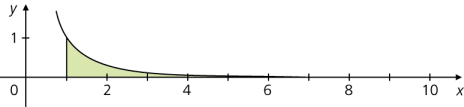
- obere (rechte) Integrationsgrenze im Unendlichen
\(\displaystyle \int\limits_{1}^{\infty } x^{-2}\,\text dx = \lim_{b \to \infty} \int\limits_{1}^{b} x^{-2}\, \text dx = \lim_{b \to \infty} \left[- x^{-1} \right]^b_1 = \lim_{b \to \infty} (- b^{-1} + 1) = 1\)
- untere (linke) Integrationsgrenze im Unendlichen
\( \displaystyle \int\limits_{-\infty }^{1} \text e^x\,\text dx = \lim_{a \to -\infty} \int\limits_{a}^{1} \text e^x\,\text dx = \lim_{a \to -\infty} [\text e^x ]^1_a = \lim_{a \to -\infty} ( \text e^1 - \text e^a ) = \text e\)
- beide Integrationsgrenzen im Unendlichen
Für die Gauß’sche Integralfunktion \(\displaystyle \Phi (x) = \frac{1}{\sqrt{2\pi }} \cdot \int\limits_{-\infty }^{x} e^{-\frac{1}{2}\cdot t^2}\,\text dt \ \ (x \in \mathbb{R})\) gilt: \(\displaystyle \frac{1}{\sqrt{2\pi }} \cdot \int\limits_{-\infty }^{+\infty } \text e^{-\frac{1}{2}\cdot t^2}\, \text dt = 1\)
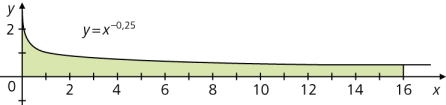
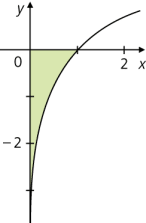
- Integrand divergiert an Grenze des Integrationsbereichs
\(\displaystyle \int\limits_{0}^{16}x^{-0,25}\, \text dx = \lim_{t \to 0 + 0}\int\limits_{t}^{16}x^{-0,25}\, \text dx = \lim_{t \to 0 + 0} \left[\frac{x^{-0,25+1}}{-0,25+1}\right]^{16}_t=\lim_{t \to 0 + 0} \left(\frac{4}{3}\cdot 16^{0,75}-\frac{4}{3}\cdot t^{0,75}\right)=\frac{32}{3}\)\(\displaystyle \int\limits_{0}^{1}\ln x\, \text dx = -\int\limits_{-\infty }^{0}\text e^x\, \text dx = - 1\)