Eine Matrix, mit der man den Übergang eines durch einen Zufallsvektor beschriebenen Systems von einem Zustand zum nächsten berechnen kann. Dies ist dann möglich, wenn man die gegenseitige Beeinflussung der Systemgrößen, also der Zufallsvariablen, welche die Komponenten des Zufallsvektors bilden, mit einem lineares Gleichungssystem beschreiben kann.
Konstante äußere Einflüsse werden durch die Addition eines festen Vektors berücksichtigt (dieser Fall wird in der Schule aber nur selten behandelt).
Wenn man das Modell über sehr viele Zeitschritte betrachtet, also einen anfänglichen Startvektor mit einer hohen Potenz der Übergangsmatrix multipliziert, kann es passieren, dass sich der Wert des Vektor einem sog. Fixvektor immer weiter annähert. Die Matrix, die den Übergang vom Startvektor zum Fixvektor beschreibt, nennt man dann Grenzmatrix.
Beispiel:
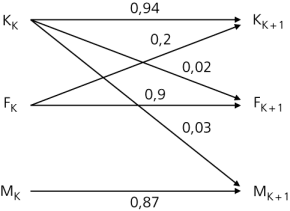
Der Zustandsvektor \(\overrightarrow{v_k} = \begin{pmatrix} K_k \\ F_k \\ M_k \end{pmatrix}\) gibt die Anzahl der Kinder, Frauen und Männer in Deutschland im Jahr k an. Die Veränderungen (Übergänge) im Zeitraum eines Jahres (Kinder werden erwachsen, Frauen bekommen Kinder, Sterbefälle treten auf) können in einem Pfeildiagramm veranschaulicht werden:
Die Beziehungen zwischen den Zufallsvariablen K, F und M werden durch das folgende Gleichungssystem modelliert:
\(\begin{matrix} 0,94 K_k &+& 0,2 F_k &+& 0 M_k &=& K_{k + 1} \\ 0,02 K_k &+& 0,9 F_k &+& 0 M_k &=& F_{k + 1} \\ 0,03 K_k &+& 0 F_k &+& 0,87 M_k &=& M_{k + 1} \end{matrix}\)
In Matrixschreibweise sieht das dann so aus:
\(\begin{pmatrix} K_{k + 1} \\ F_{k + 1} \\ M_{k + 1} \end{pmatrix} = \begin{pmatrix} 0,94 & 0,2 & 0 \\ 0,02 & 0,9 & 0 \\ 0,03 & 0 & 0,87 \end{pmatrix} \begin{pmatrix} K_{k} \\ F_{k} \\ M_{k} \end{pmatrix}\)
und \(A = \begin{pmatrix} 0,94 & 0,2 & 0 \\ 0,02 & 0,9 & 0 \\ 0,03 & 0 & 0,87 \end{pmatrix}\) ist die Übergangsmatrix dieses Systems.
Die jährliche Zuwanderung ist ein Beispiel für einen konstanten Vektor, sofern sie unabhängig von den Systemgrößen ist und sich nicht mit der Zeit verändert. Man könnte dann die Entwicklung der Bevölkerungsstatistik mit der folgenden (inhomogenen) Matrixgleichung modellieren:
\(\begin{pmatrix} K_{k + 1} \\ F_{k + 1} \\ M_{k + 1} \end{pmatrix} = \begin{pmatrix} 0,93 & 0,19 & 0 \\ 0,02 & 0,88 & 0 \\ 0,02 & 0 & 0,83 \end{pmatrix} \begin{pmatrix} K_{k} \\ F_{k} \\ M_{k} \end{pmatrix} + \begin{pmatrix} 0,05 \\ 0,06 \\ 0,08 \end{pmatrix}\)