Bei Extremwertaufgaben sucht man mithilfe der Differenzialrechnung möglichst große oder kleine Werte von interessierenden Größen, z. B. das kleinstmögliche Volumen eines Paketstapels, die größte Weite eines Ballwurfs oder der schnellste Weg zu einem Nichtschwimmer, der in den Badesee gefallen ist. Man nennt so etwas auch ein Optimierungsproblem.

▶ Allgemeines Vorgehen

  1. „Mathematische“ Formulierung der Aufgabe: Alltagssprachliche Begriffe in mathematische übersetzen, beschriftete Skizze, gegebene Größen und Nebenbedingungen auflisten

  2. Funktionsgleichung für die optimierende Größe in Abhängigkeit von den anderen Variablen, Variablenzahl mithilfe der Nebenbedingungen reduzieren

  3. Definitionsmenge D festlegen

  4. lokale Extrema bestimmen

  5. prüfen, ob an den Rändern von D ein bisher übersehenes globales Maximum oder Minimum vorliegt

Beispiel:
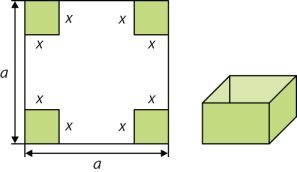
Aus einem Stück Pappe (60 × 70 cm2) soll eine offene Schachtel mit quadratischer Grundfläche und möglichst großem Volumen gefaltet werden.

1. Mathematisierung der Aufgabe
Vorüberlegungen: Die Schachtel soll einen quadratischen Boden haben. Daher kann von dem Stück Pappe nur ein quadratisches Stück mit der Seitenlänge 60 cm verwendet werden. Ausgangspunkt ist also ein Quadrat mit Seitenlänge a = 60 cm. Das entstehende Schachtelvolumen V soll maximal werden. Gesucht ist daher die Länge x eines zu entfernenden Quadrats in cm.

 

2. Funktionsgleichung
Die Schachtel hat nach dem Entfernen der Eckquadrate und dem Zusammenfalten die Höhe x und eine quadratische Grundfläche mit der Seitenlänge a – 2x. Damit ergibt sich die Funktionsgleichung für V(x) mit dem zusätzlichen Parameter a:

\(V (x) = (a - 2x )^2 \cdot x = ( a^2 - 4ax + 4x^2 ) \cdot x = 4 x^3 - 4a x^2 + a^2 x\).

3. Definitionsbereich
x kann alle Werte zwischen 0 und 30 cm annehmen, also gilt \(D = ]0; 30[\).

4. Bestimmung der lokalen Extrema
Aus \(V (x) = (a - 2x )^2 \cdot x = 4 x^3 - 4a x^2 + a^2 x\) folgt:

\(V' (x) =12 x^2 - 8ax + a^2\) und \(V'' (x) = 24x - 8a\).

Notwendige Bedingung für Extrema: \(V' (x) = 0\).

\(V' (x) = 0 \Leftrightarrow 12 x^2 - 8ax + a^2 = 0\).

Mit der Mitternachtsformel ergibt sich:

\(\displaystyle x_{1; 2}= \frac{8a\pm \sqrt{64a^2-4\cdot 12\cdot a^2}}{2\cdot 12}=\frac{2a\pm a}{6}\) bzw. \(\displaystyle x_1=\frac{a}{6}\) oder \(\displaystyle x_2=\frac{a}{2}\) 

\(\displaystyle x_2 = \frac{a}{2} = 30\) liegt nicht im Definitionsbereich \(D = ]0; 30[\), also bleibt nur die Lösung \(\displaystyle x_1=\frac{a}{6}\).

Wegen \(\displaystyle V'' \left( \frac{a}{6} \right) = 24 \cdot \frac{a}{6} - 8a = - 4a < 0\) liegt bei \(\displaystyle x_1 = \frac{a}{6}\) Rechtskrümmung und damit ein lokales Maximum von V vor: Mit a = 60 cm ist x1 = 10 cm und V(x1) = 16.000 cm3 = 16 Liter.

5. Bestimmung des globalen Maximums
An den Rändern Rand von D gilt: \(\displaystyle \lim_{x \to 0}V(x) = \lim_{x \to 30}V(x) = 0\).

Da V(x) in \(D = ]0; 30[\) differenzierbar ist, gibt es in D außer bei x1 = 10 cm kein weiteres Maximum.

Schlagworte

  • #Differenzialrechnung
  • #Extremwertaufgaben
  • #Optimierung