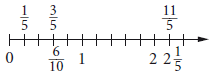Als Bruchzahlen bezeichnet man entweder einfach die rationalen Zahlen oder aber nur die nichtnegativen rationalen Zahlen, also alle Zahlen, die als Brüche mit natürlichen Zahlen in Zähler und Nenner (natürlich ohne 0 im Nenner!) geschrieben werden können. Im zweiten Fall fasst man die Bruchzahlen in der Menge \(\displaystyle \mathbb B = \left\{ \left.\frac m n \right| m \in \mathbb N, \ n \in \mathbb N \setminus\{0\}\right\} \equiv \mathbb Q_0^+\) zusammen.
Anmerkung: Welche Variante gilt, hängt im Wesentlichen davon ab, ob in deinem Bundesland erst die Bruchrechnung oder erst die negativen Zahlen eingeführt werden. Kommen die Brüche zuerst dran, rechnet man mit ihnen nur in der Menge \(\mathbb B\), kennt man die negativen Zahlen schon, dann kann man gleich in ganz \(\mathbb Q\) loslegen.
Jeder Bruchzahl ist genau ein Punkt auf dem Zahlenstrahl zugeordnet.
Umgekehrt gehören aber zu jeder Bruchzahl auf dem Zahlenstrahl unendliche viele weitere Brüche, die sich durch erweitern oder kürzen ineinander umwandeln lassen.
Beispiel:
\(\displaystyle \frac 1 5 = \frac {2}{10} = \frac {5}{25} = \ldots \)