-
Aufgabe 1
Dauer: 8 Minuten 6 PunkteBestimme die fehlenden Größen für die Kreise \(k\).
- \(r\): Radius des Kreises \(k\)
- \(U\): Umfang des Kreises \(k\)
- \(A\): Flächeninhalt des Kreises \(k\)
\(r\) 14 mm \(U\) \(30\pi\) m \(A\) 36 cm² -
Aufgabe 2
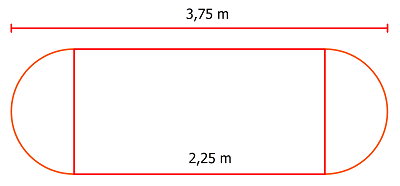
Dauer: 7 Minuten 6 PunkteDie Abbildung zeigt die Maße einer Tischplatte.
- Berechne die Tischfläche.
- Beim Eindecken für eine Festtafel rechnet man etwa \(75\ \text{cm}\) Platz pro Person. Für wie viele Gäste kann an diesem Tisch eingedeckt werden?
-
Aufgabe 3
Dauer: 6 Minuten 3 PunkteBerechne den Kreisbogen \(b\) und den Flächeninhalt \(A\) des Kreisausschnitts mit dem Mittelpunktwinkel \(\alpha=20^°\) und dem Kreisradius \(r= 6\text{ cm}\).
-
Aufgabe 4
Dauer: 6 Minuten 4 PunkteDer Kreis \(k_2\) hat einen doppelt so großen Flächeninhalt wie der Kreis \(k_1\). Der Radius von \(k_1\) ist 30 cm lang. Wie lang ist der Radius von \(k_2\)?
-
Aufgabe 5
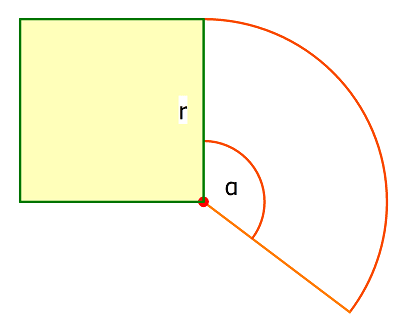
Dauer: 7 Minuten 5 PunkteWie groß muss der Winkel \(\alpha \) sein, damit der dazugehörige Kreissektor den gleichen Flächeninhalt hat wie das Quadrat mit der Kantenlänge \( r\)?
-
Aufgabe 6
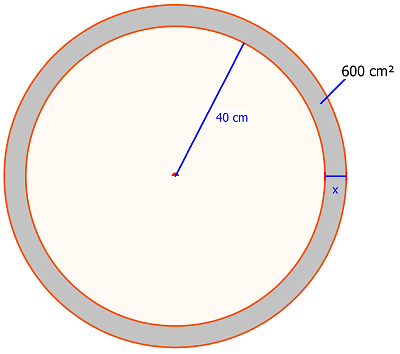
Dauer: 9 Minuten 6 PunkteEin Kreisring hat einen Flächeninhalt von 600 cm². Der Radius des inneren Kreises beträgt 40 cm. Welche Dicke hat der Kreisring?
-
Aufgabe 1
Bestimme die fehlenden Größen für die Kreise \(k\).
- \(r\): Radius des Kreises \(k\)
- \(U\): Umfang des Kreises \(k\)
- \(A\): Flächeninhalt des Kreises \(k\)
\(r\) 14 mm \(U\) \(30\pi\) m \(A\) 36 cm²