• Aufgabe 1

    8 Minuten 6 Punkte
    einfach

     

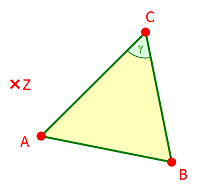
       a) Führe eine zentrische Streckung (Streckfaktor k = 2) des Dreiecks ABC vom Streckzentrum Z aus durch. Bezeichne alle Punkte und Winkel.

       b) Was lässt sich über die folgenden Größenpaare aussagen?

    • Länge der Seite \(\overline{BC}\) und Länge der Seite \(\overline{B'C'}\)?
    • Länge der Seite \(\overline{ZB}\) und Länge der Seite \(\overline{Z'B'}\)?
    • \(\gamma \) und \(\gamma'\)?
    • \(\overline{AC}:\overline {AB}\) und \(\overline{A'C'}:\overline {A'B'}\)?
    • Flächeninhalt des Dreiecks ABC und Flächeninhalt des Dreiecks A'B'C'?

  • Aufgabe 2

    5 Minuten 3 Punkte
    einfach

    Zwei Vierecke ABCD und A'B'C'D' haben folgende Seitenlängen:

    a = 5,4 cm, b = 4,2 cm, c = 3 cm, d = 3,2 cm,

    a' = 8,1 cm, b' = 6,3 cm, c' = 4,5 cm, d' = 4,8 cm.

    Sind die beiden Vierecke ähnlich? Begründe deine Antwort!

  • Aufgabe 3

    12 Minuten 10 Punkte
    einfach

    Bestimme jeweils die Strecke a bzw. b.

       a)

       b)

       c)

     

  • Aufgabe 4

    6 Minuten 3 Punkte
    mittel

    Wie hoch ist ein Baum, der einen 20 m langen Schatten wirft, wenn gleichzeitig der Schatten des 1,80 m großen Försters 1,20 m lang ist?

  • Aufgabe 5

    6 Minuten 4 Punkte
    mittel

    Um die Höhe eines alten Wasserturms zu ermitteln, werden zwei Stäbe mit den Längen 0,70 m und 1,00 m so aufgestellt, dass man über die Spitzen der Stäbe die Spitze des Wasserturms anpeilen kann. Der längere Stab steht 100 m vom Turm entfernt. Der kürzere Stab noch mal 1,5 m weiter. Wie hoch ist der Turm?

     

  • Aufgabe 6

    8 Minuten 5 Punkte
    mittel

    Um die Breite eines Flusses bestimmen zu können, hat man die in der Skizze angegebenen Längen gemessen.

       a) Erläutere das Vorgehen. Vervollständige dazu die Skizze.

       b) Wie breit ist der Fluss?