Ein kartesisches Koordinatensystem (nach dem Mathematiker und Philosophen René Descartes, der sich lateinisch „Cartesius“ nannte) zeichnet sich von anderen Koordinatensystemen durch folgende Eigenschaften aus:
- Seine Achsen sind Geraden.
- Seine Achsen stehen paarweise senkrecht aufeinander.
- Seine Achsen schneiden sich im selben Punkt, dem Ursprung (dies ist allerdings auch bei anderen Koordinatensystem fast immer der Fall).
In zwei Dimensionen nennt man das kartesische Koordinatensystem auch Achsenkreuz. Es dient vor allem zur Darstellung von Funktionsgraphen, insbesondere auch bei Kurvendiskussionen. Die zwei Koordinatenachsen teilen die Ebene in vier Felder, die man aus historischen Gründen Quadranten nennt. Wenn man die Achsen um 45° um den Ursprung dreht, erhält man die sog. erste und zweite Winkelhalbierende. Sie sind die Graphen der Funktionen y = x bzw. y = –x.
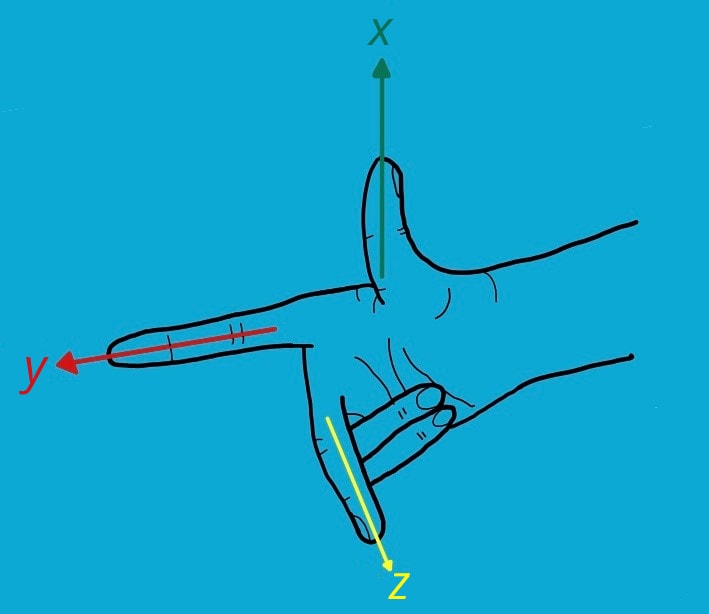
In drei Dimensionen verwendet man kartesische Koordinatensysteme in der Analytischen Geometrie zur Darstellung und Untersuchung von Körpern, Geraden und Ebenen sowie von Abständen und Lagebeziehungen zwischen ihnen. Die Achsen nennt man meist entweder x-Achse, y-Achse und z-Achse oder x1-, x2- und x3-Achse. Dabei gibt es, anders als in zwei Dimensionen, zwei Möglichkeiten: Die dritte Achse kann „in die Papierebene hinein“ oder „aus der Papierebene hinaus“ zeigen. Beide Darstellungen gehen durch eine Raumspiegelung ineinander über. Die allgemeine Konvention ist, dass x, y und z bzw. x1, x2 und x3 so orientiert sind wie Daumen, Zeigefinger und Mittelfinger der rechten Hand:
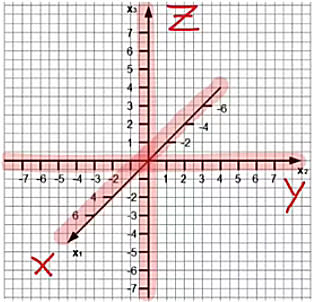
Für das Koordinatensystem bedeutet dies, dass für den Fall, dass x- und y-Achse wie beim zweidimensionalen Achsenkreuz „in der Papierebene“ liegen sollen, die z-Achse nach „vorne“ bzw. „aus der Papierebene heraus“ zeigen muss. Anders als beim Zeichnen von Schrägbildern ist es übrigens nicht unbedingt die beste Wahl, Längen auf der dritten Achsen zu halbieren. Es kann auch sinnvoll sein (gerade wenn man Karokästchen hat), einen Verkürzungsfaktor \(\frac 1 {\sqrt 2}\) zu wählen, wie die folgende Skizze zeigt, bei der y- und z-Achse bzw. x2- und x3-Achse in der Papierebene liegen.