Ein Schwingkreis ist ein (geschlossener) Stromkreis, in dem eine Spule und ein Kondensator in Reihe geschaltet sind. Ein realer Schwingkreis besitzt immer auch einen Ohm’schen Widerstand, dies vernachlässigt der ideale Schwingkreis jedoch wegen der einfacheren Berechnung.
Werden die Ladungen im Schwingkreis einmal in Bewegung versetzt, führen Strom und Spannung harmonische Schwingungen aus, wobei die Energie zwischen dem Kondensator (elektrische Energie) und der Spule (magnetische Energie) hin- und herschwingt. Strom und Spannung sind dabei um 90° bzw. \(\pi/2\) phasenverschoben. Ein realer Schwingkreis mit Widerstand R unterscheidet sich hiervon nur darin, dass die Schwingungen mehr oder weniger stark gedämpft werden und die elektromagnetische Energie allmählich in Wärmeenergie umgewandelt wird, bis die Schwingung zum Erliegen kommt.
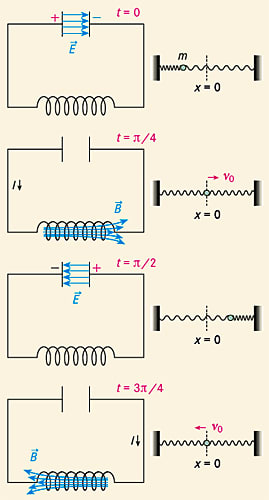
Um das Geschehen zu erklären, nehmen wir an, dass zu Anfang der Kondensator aufgeladen (elektrisches Feld im Kondensator) und die Spule stromlos ist (kein magnetisches Feld in der Spule). Eine Schwingungsperiode besteht dann aus den folgenden vier Phasen:
- In Phase 1 entlädt sich der Kondensator über einen durch die Spule fließenden Strom. Dabei steigen sowohl die Stromstärke I wegen der in der Spule induzierten Gegenspannung \(U_\text{ind} = L \cdot \dfrac {\text d I}{\text d t}\) nur allmählich an (L: Induktivität der Spule). Das elektrische Kondensatorfeld E nimmt ab, das magnetische Spulenfeld B zu.
- Zu Beginn von Phase 2 ist der Kondensator gerade entladen, und durch die Spule fließt der maximale Entladestrom, für den \(\dfrac {\text d I}{\text d t} = 0\) ist (E = 0, B maximal). Also ist die Induktionsspannung gleich 0. Der Strom fließt zunächst weiter und lädt den Kondensator in umgekehrter Polung auf. Die sich aufbauenden Kondensatorspannung (mit umgekehrtem Vorzeichen) wirkt die wegen des abnehmenden Stroms ebefalls umgekehrt gepolte Induktionsspannung entgegen.
- Zu Beginn der Phase 3 ist der Kondensator erneut vollständig aufgeladen (aber mit umgekehrter Polung in Vergleich zu Phase 1) und der Strom abgeklungen (E maximal, B = 0). Es folgen das erneute Entladen (Phase 3) und Aufladen (Phase 4) des Kondensators genau wie in den Phasen 1 und 2, nur mit umgekehrten Richtungen bei Strömen und Spannungen.
Mathematisch kann man das mithilfe einer Differenzialgleichung modellieren, auf die man folgendermaßen kommt. Die Induktionsspannung und die Spannung am Kondensator müssen sich wegen der Kirchhoff’schen Maschenregel zu 0 addieren:
\(U_\text{ind.} + U_\text{Kond.} = L \cdot \dfrac{\text d I}{\text d t} + \dfrac Q C = 0\)
(Q: Ladung, C: Kapazität des Kondensators).Mit \(I = \dfrac {\text d Q}{\text d t}\) erhält man daraus eine Differenzialgleichung für die Ladung am Kondensator:
\(L \cdot \dfrac{\text d^2 Q}{\text d t^2} + \dfrac Q C = 0\)
Die Lösungen dieser Differenzialgleichung sind Sinus- und Kosinusfunktionen, wie man durch Ausprobieren schnell nachprüft (die Ableitung des Sinus ist der Kosinus und dessen Ableitung ist „minus Sinus“).
Also muss die Ladung sinusförmig hin- und herschwingen und entsprechend Stromstärke und Spannung.
Indem man an einen Schwingkreis eine Wechselspannung anlegt, können erzwungene Schwingungen erzeugt werden. Es treten dann die typischen Resonanzeffekte auf. Erzwingt man eine Schwingung mit der Eigenfrequenz des Schwingkreises, wirkt der Schwingkreis in einer Schaltung wie ein sehr großer Widerstand. In dieser Anordnung bezeichnet man ihn deshalb auch als Sperrkreis. Schwingkreise werden in der Elektrotechnik, insbesondere in der Rundfunktechnik, bei elektronischen Filtern und Verstärkern eingesetzt. Eine Antenne, die elektromagnetische Wellen abstrahlt bzw. empfängt, kann man als „aufgebogenen“ Schwingkreis auffassen.
Übrigens: Wie in der Abb. angedeutet, sind die Vorgänge im Schwingkreis ganz analog zu einer mechanischen Schwingung, etwa eines Federpendels. Die elektrische Energie im Kondensator entspricht dabei der potenziellen Spannenergie der Feder.