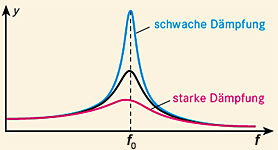
Resonanz (von lat. resonare „nachklingen“) ist das Mitschwingen eines schwingungsfähigen Systems (Schwinger), das an ein anderes schwingendes System, den Erreger, gekoppelt ist. Speziell meint man damit meist den Fall, dass bei einer Erregerfrequenz nahe der sog. Resonanzfrequenz oder Eigenfrequenz f0 des Schwingers eine besonders starke Schwingung bis hin zur „Resonanzkatastrophe“ ausgelöst wird. Die Abhängigkeit der Amplitude A der erzwungenen Schwingung von der Erregerfrequenz f wird durch die Resonanzkurve dargestellt (Abb.).
Als Beispiel betrachten wir ein senkrecht aufgehängtes Federpendel, auf dessen oberes Ende periodisch eine Kraft einwirkt.
- Ist die Erregerfrequenz viel kleiner als die Eigenfrequenz des schwingenden Systems, stimmt die Amplitude der erzwungenen Schwingung des Pendelkörpers mit der Amplitude der äußeren Kraft überein. Der Körper schwingt auf und ab, ohne dass sich die Feder verformt.
- Steigert man die Anregungsfrequenz nach und nach, so vergrößert sich die Amplitude der Schwingung des Körpers.
- Wenn schließlich die Erregerfrequenz mit der Eigenfrequenz des Federsystems übereinstimmt, erreicht die Amplitude einen Maximalwert (Resonanzfall). Je geringer die Dämpfung der Schwingung ist, desto größer ist dieser Maximalwert. Bei zu kleiner Dämpfung kann der Resonanzfall zur Zerstörung des schwingenden Systems führen.
- Bei weiterer Erhöhung der Erregerfrequenz nimmt die Amplitude wieder ab.
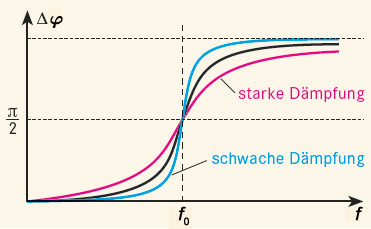
Mit der Änderung der Erregerfrequenz ändert sich auch die Phasenbeziehung zwischen der Erregerschwingung und der Schwingung des Körpers (Abb.). Während für kleine Frequenzen die Erreger- und Körperschwingungen in Phase ablaufen, verschieben sie sich mit zunehmender Frequenz um einen Winkel \(\Delta \varphi\) gegeneinander, bis im Resonanzfall die Erregerschwingung um 90° bzw. um \(\pi/2\) der erzwungenen Schwingung vorauseilt. Bei weiterer Vergrößerung nimmt die Phasendifferenz weiter zu und erreicht schließlich bei sehr hohen Frequenzen einen Wert von 180° bzw. \(\pi\), d. h., Erreger und und Schwinger bewegen sich gegenphasig. Die Phasenänderung erfolgt umso abrupter im Bereich des Resonanzfalls, je geringer die Dämpfung ist.
Resonanz tritt in unzähligen Gebieten der Natur und der Technik auf. Bei manchen technischen Anwendungen, z. B. bei Motoren, den meisten Maschinen oder Bauwerken, versucht man, sie zu vermeiden. In anderen Systemen, z. B. elektrischen Schwingkreisen, ist sie erwünscht. Die Klangerzeugung vieler Musikinstrumente und der menschlichen Stimme beruht ebenfalls auf Resonanz.