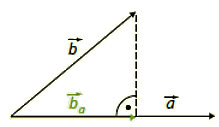
Eine senkrechte Projektion (Orthogonalprojektion) bildet Punkte so auf eine Ebene oder Gerade ab, dass die Verbindungslinie zwischen Punkt und Bildpunkt senkrecht auf der Projektionsebene/-gerade steht. Man ignoriert also in gewisser Weise alle Komponenten außerhalb der Projektionsebene/-gerade und interessiert sich nur für den Anteil in der Projektionsebene/-gerade. Auf diese Weise wird aus einem dreidimensionalen Problem ein zwei- oder eindimensionales.
Wenn der \(\vec b\) Ortsvektor von Punkt B ist und \(\vec a\) der Richtungsvektor der Geraden, auf die B projiziert werden soll (\(\vec a^0\) ist der Einheitsvektor in \(\vec a\)-Richtung), dann gilt für die senkrechte Projektion \(\vec b_a\) von \(\vec b\) auf die Gerade in \(\vec a\)-Richtung:
\(\displaystyle \vec b_a = \left(\vec b \circ \vec a^0\right) \cdot \vec a^0= \frac{\vec b \circ \vec a}{|\vec a|^2}\cdot \vec a\)