Der Schattenpunkt ist die Projektion eines Punkts P im Raum auf eine Fläche wie die horizontale Ebene (den „Fußboden“) oder eine (Haus-)Wand. Wenn die Lichtquelle das Sonnenlicht ist, kann man von parallel einfallendem Licht ausgehen, also einer Parallelprojektion in Richtung des Vektors \(\vec v\). Der Schattenpunkt ist dann der Schnittpunkt der Geraden durch den Punkt P mit dem Richtungsvektor \(\vec v\) und der angegebenen Fläche. Bei einer punktförmigen Lichtquelle L wird die Projektionsrichtung durch den Differenzvektor von P und L angegeben.
Beispiel:
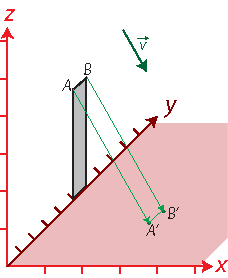
Die Abbildung zeigt die Schattenpunkte A’ und B’ auf der xy-Ebene bei parallelem Lichteinfall in Richtung des Vektors \(\vec v\).