Das Newton-Verfahren (nach Isaac Newton) ermöglicht die näherungsweise Berechnung von Nullstellen einer Funktion.
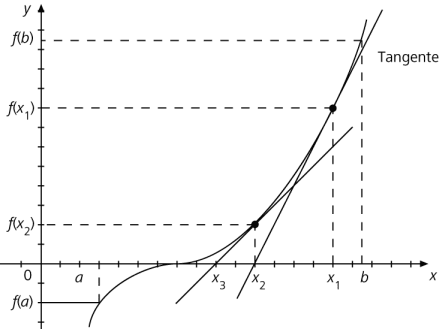
Die Grundidee bei dieser Methode ist es, die gegebene Funktion in einem Intervall [a; b], in dem sicher eine Nullstelle liegt, durch ihre Tangente in einem „Startpunkt“ P1(x1|f(x1)) (mit a < x1 < b) anzunähern.
Die Nullstelle x2 dieser Tangente ist eine erste Näherung für die gesuchte Nullstelle der Funktion. Der Trick ist dann einfach, den Punkt P2(x2|f(x2)) als Ausgangspunkt für den nächsten Berechnungsschritt zu verwenden usw. Das Newton-Verfahren ist damit ein iteratives Rechenverfahren.
Das Verfahren wird so lange wiederholt bzw. „iteriert“, bis die Näherungslösungen sich weniger als eine vorgegebene Genauigkeit voneinander unterscheiden.
Die Tangentensteigung im n-ten Iterationsschritt ist am Punkt Pn(xn|f(xn))
\( m_{\text t,\,n} = f' ( x_n ) = \dfrac{f(x_n)}{x_n-x_{n+1}}\)
Daraus erhält man als nächste, also (n + 1)-te Näherung der gesuchten Nullstelle:
\(\displaystyle x_{n + 1} = x_n - \frac{f(x_n)}{f'(x_n)} \ \ ( f' (x_n ) \neq 0)\).
Diese Folge der Näherungswerte konvergiert immer dann gegen die Nullstelle, wenn der Startwert x1 genügend dicht an der gesuchten Nullstelle liegt.
Beispiel:
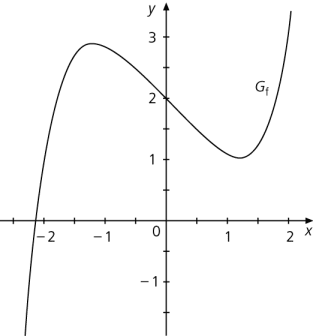
\( f : x \mapsto 0,1 x^5 - x + 2\), Näherung auf sechs Dezimalen genau.
Erste Abschätzungen ergeben, dass eine Nullstelle im Intervall [–2,5; –2] liegen muss.
Erste Ableitung: \(f' (x) = 0,5 x^4 - 1\)
Startwert: x1 = –2
Rekursive Berechnung der Folge (xn) der Iterationswerte: \(\displaystyle x_{n + 1} = x_n-\frac{f(x_n)}{f'(x_n)} =x_n-\frac{{0,1x_n}^5-x_n+2}{{0,5x_n}^4-1}\).
Beim 5. Iterationsschritt ist die gewünschte Genauigkeit erreicht: Die Nullstelle liegt bei \(x \approx - 2,101. 819\).