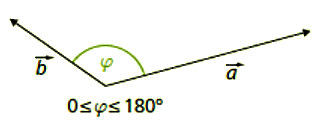
Für den Winkel \(\varphi\) zwischen Vektoren \(\vec a\) und \(\vec b\) gilt
\(\displaystyle \cos \varphi = \frac{\vec a \circ \vec b}{|\vec a | \cdot | \vec b|} \ \ \Leftrightarrow \ \ \varphi = \arccos \frac{\vec a \circ \vec b}{|\vec a | \cdot | \vec b|} \)
(„\(\circ\)“ ist das Skalarprodukt und arccos der Arkuskosinus, also die Umkehrfunktion des Kosinus.)
Beispiel:
- \(\overrightarrow{a} = \left(\begin{array}{c}{-3}\\{4}\end{array}\right) , \ \ \overrightarrow{b} = \left(\begin{array}{c}{12}\\{5}\end{array}\right)\)
\(\overrightarrow{a}\circ \overrightarrow{b} = \left(\begin{array} {c}{-3}\\{4}\end{array}\right)\circ \left(\begin{array} {c}{12}\\{5} \end{array}\right)= -3 \cdot 12 + 4 \cdot 5 = -16\)
\(|\overrightarrow{a}| = \sqrt{(-3)^2+4^2} = 5, \ \ | \overrightarrow{b}| = \sqrt{12^2+5^2} = 13\)
\(\displaystyle \cos \phi = \frac{\overrightarrow{a}\circ \overrightarrow{b}}{|\overrightarrow{a}|\cdot | \overrightarrow{b}|} = \frac{-16}{5 \cdot 13} \ \Rightarrow \ \phi \approx 104^{\circ}\)
Zwei Vektoren \(\vec a\) und \(\vec b\) stehen aufeinander senkrecht (sind orthogonal), wenn sie einen Winkel von \(\varphi = 90^\circ\) einschließen. Ihr Skalarprodukt ist dann wegen \(\cos 90^\circ = 0\) ebenfalls null: \(\vec a \circ \vec b = 0\).
Wenn zwei Einheitsvektoren (als Vektoren mit dem Betrag 1) zueinander orthogonal sind, nennt man sie orthonormiert.
Zwei Vektoren \(\vec a\) und \(\vec b\) sind parallel, wenn der Winkel zwischen ihnen \(\varphi = 0^\circ\) ist. Dann ist \( \cos \varphi = 1\) und es gilt \(\vec a \circ \vec b = |\vec a | \cdot | \vec b|\).