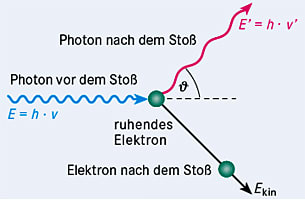
Der Compton-Effekt wurde 1922 von Arthur H. Compton und besteht in der Änderung von Frequenz bzw. Wellenlänge elektromagnetischer Wellen bei der elastischen Streuung an Elektronen.
Trifft ein Photon auf ein ruhendes Elektron, gibt es analog zum klassischen elastischen Stoß zweier Teilchen Energie an das Elektron ab, die dieses als kinetische Energie Ekin aufnimmt:
\(E' = E - E_\text{kin}\)
wobei E und \(E'\) die Photonenenergie vor bzw. nach dem Stoß bedeuten. Wegen \(E = h \cdot f\) bedeutet der Energieverlust beim Stoß eine geringere Frequenz f nach dem Stoß, es gilt
\(h\cdot f' = h\cdot f - E_\text{kin} \quad \Rightarrow \quad f' = f - \dfrac {E_\text{kin} } h\)
(h: Planck’sches Wirkungsquantum).
Für die Wellenlänge \(\lambda\) des Photons gilt \(\lambda = \dfrac c n\) bzw. \(\lambda' = \dfrac c n'\) (c: Lichtgeschwindigkeit). Die Wellenlängenänderung hängt vom Streuwinkel \(\vartheta\) ab. Man bezeichnet sie als Compton-Verschiebung. Es ergibt sich unter Anwendung des Impulssatzes:
\(\Delta \lambda = \lambda' - \lambda = \lambda_\text C \cdot (1 - \cos \vartheta)\)
\( \lambda_\text C = \dfrac h {m_\text e \cdot c}\approx 2,426 \cdot 10^{-12}\,\text m\) ist die Compton-Wellenlänge des Elektrons (me: Elektronenmasse). Jedes Teilchen hat eine eigene Compton-Wellenlänge, die man berechnet, indem in die Formel statt me die entsprechende Teilchenmasse eingesetzt wird.
Beim inversen Compton-Effekt übertragen energiereiche Elektronen ihre Energie auf Photonen. Solche Elektronen kommen z. B. in intergalaktischen Bereichen vor. Treffen sie auf die langwelligen Photonen der kosmischen Hintergrundstrahlung, so wird diese in energiereiche und damit kurzwellige Röntgenstrahlung verwandelt.