Elastischer Stoß und inelastischer Stoß

Allgemein ist ein Stoß ein physikalischer Vorgang, bei dem zwei oder mehrere Objekte, die Stoßpartner, sich aufeinander zubewegen, miteinander in Wechselwirkung treten und sich anschließend mit in Betrag und Richtung veränderter Geschwindigkeit weiterbewegen (je nach Blickwinkel kann die veränderte Geschwindigkeit auch 0 sein!). Bei Elementarteilchen spricht man auch oft von Streuung.

In der Mechanik untersucht man meistens den Stoß von zwei starren Körpern. Während der sehr kurzen Stoßzeit wirken sehr große Stoßkräfte, und die Impulse der Stoßpartner ändern sich praktisch augenblicklich. Die Senkrechte auf die Berührungsebene nennt man die Stoßnormale.

Der S. von zwei Körpern heißt zentraler Stoß, wenn die Stoßnormale durch die Schwerpunkte beider Körper geht, sie sich also „mittig“ treffen. Weiterhin unterscheidet man den geraden Stoß (beide Körper bewegen sich vor dem S. in Richtung der Stoßnormalen) vom schiefen Stoß.

Bei allen Stößen gilt der Impulssatz, d. h. die Vektorsumme aller Impulse ist vor und nach dem Stoß gleich. Wenn außerdem auch die Bewegungsenergie erhalten ist, handelt es sich um einen elastischen, andernfalls um einen inelastischen Stoß. Bei Letzterem wird kinetische Energie meist in Formänderungsarbeit überführt, die stoßenden Körper werden deformiert oder zerbrochen. Der größte Teil der umgewandelten Energie wird letztlich zu Wärmeenergie.

Zwei Fälle sind besonders gut zu behandeln:

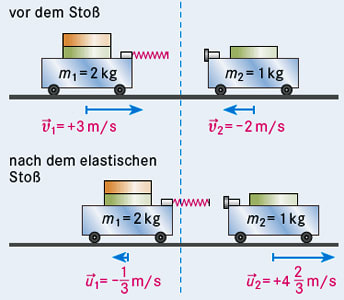
• Elastischer gerader zentraler Stoß zweier Körper
  Es seien m₁, m₂ die Massen und \(v_1\), \(v_2\) die Geschwindigkeiten der Körper 1 und 2 vor, u₁ und u₂ die Geschwindigkeiten nach dem Stoß (Abb.). Da der Stoß gerade und zentral ist, man kann eindimensional rechnen und es gelten der Impuls- und der (kinetische) Energiesatz:
  \(m_1v_1 + m_2v_2 = m_1u_1 + m_2u_2 \\ \dfrac 1 2 m_1v_1^2 + \dfrac 1 2 m_2v_2^2 = \dfrac 1 2 m_1u_1^2 + \dfrac 1 2 m_2u_2^2\)
  Für die Geschwindigkeiten nach dem Stoß gilt dann:
  \(u_1 = \dfrac { 2m_2v_2 + v_1(m_1 - m_2) }{ m_1 + m_2 } \\ u_2 = \dfrac { 2m_1v_1 + v_2(m_2 - m_1) }{ m_1 + m_2 } \)
  Wenn beide Körper die gleiche Masse haben (m₁ = m₂ = m), wird u₁ = \(v_2\) und u₂ = \(v_1\). Stößt ein leichter Körper m₁ gegen einen ruhenden Körper mit sehr großer Masse m₂, etwa gegen eine Wand, dann gilt u₁ = –\(v_1\), der leichte Körper fliegt mit gleichem Geschwindigkeitsbetrag zurück.
   
  

  

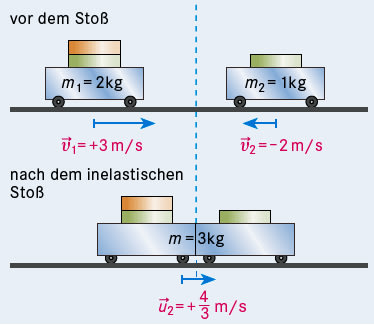
• Vollkommen inelastischer gerader zentraler Stoß zweier Körper
  In diesem Fall gilt nur der Impulssatz, die kinetische Energie bleibt nicht erhalten. Beim vollkommen inelastischen Stoß bleiben die beiden Körper nach dem Stop aneinander kleben und haben die gemeinsame Geschwindigkeit u₁ = u₂ = u:
  \(m_1v_1 + m_2v_2 = (m_1 + m_2)u\)
  Daraus erhält man dann
  \(u = \dfrac { m_1v_1 + m_2v_2}{ m_1 + m_2 }\)
  Bei gleichen Massen (m₁ = m₂ = m) ist die Endgeschwindigkeit das arithmetische Mittel der Anfangsgeschwindigkeiten:
  \(u = \dfrac { v_1 + v_2}{ 2 }\)