Pfadregeln

In der Wahrscheinlichkeitsrechnung zwei hilfreiche Regeln, um in einem Baumdiagramm Wahrscheinlichkeiten zu bestimmen:

• Die Produktregel (der Multiplikations- oder Produktsatz) besagt, dass die Wahrscheinlichkeit eines einzelnen Ergebnisses in einem mehrstufigen Zufallsexperiment gleich dem Produkt aller Einzelwahrscheinlichkeiten auf dem Pfad zu diesem Ergebnis ist.
• Die Additionsregel (der Additions- oder Summensatz) sagt, dass die Wahrscheinlichkeit eines Ereignisses gleich der Summe aller einzelnen Ergebniswahrscheinlichkeiten auf dieser Stufe des Baumdiagramm ist.

Beispiel:

Aus einer Urne wird zweimal ohne Zurücklegen gezogen (Urnenmodelle). In der Urne sind 9 Kugeln, (1 blaue, 3 rote und 4 schwarze).

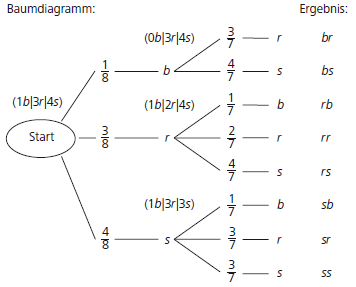
Mit der Produktregel bekommt man für das Ergebnis „erst eine schwarze, dann eine rote Kugel" die Wahrscheinlichkeit $P(sr)=\displaystyle \frac{4}{8} \cdot \frac{3}{7} = \frac{3}{14} \approx 21,4\,\%$.

Für das Ereignis „zwei schwarze oder zwei rote Kugeln“ liefert die Additionsregel $P(ss \text{ oder } rr)=\displaystyle \frac{4}{8} \cdot \frac{3}{7} + \frac{3}{8} \cdot \frac{2}{7} = \frac{9}{28} \approx 32,1\,\%$.