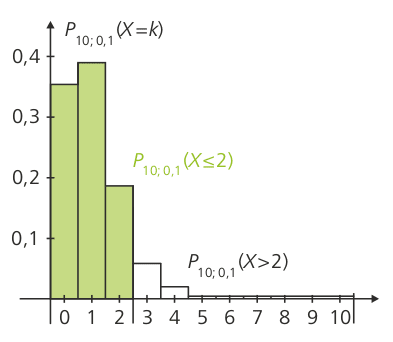Ein Alternativtest ist ein Hypothesentest (Signifikanztest), bei bei dem zwischen zwei konkreten Werten für die infragestehende Wahrscheinlichkeit p (Hypothesen H1 und H2) entschieden werden soll. Es wird also nicht wie sonst bei statistischen Tests geprüft, ob eine bestimmte Nullhypothese abgelehnt werden kann oder nicht. Dementsprechend wird für beide Hypothesen je ein Annahme- und Ablehnungsbereich formuliert.
Beispiel
Eine Firma fertigt an zwei Maschinen Schrauben. Bei der Maschine A halten erfahrungsgemäß 10 der produzierten Stücke die geforderten Toleranzen nicht ein (Ausschussstücke), bei Maschine B sind es 30. Große Stückzahlen werden hinter jeder Maschine in Schachteln verpackt, die mit Aufklebern „1. Wahl“ bzw. „2. Wahl“ bei Maschine A bzw. B versehen werden. Bei einigen Schachteln ist der Aufkleber verlorengegangen. Es soll möglichst rasch entschieden werden, ob es sich um 1. oder 2. Wahl handelt. Dazu werden aus jeder Schachtel n Stücke rein zufällig entnommen und geprüft (Stichprobe vom Umfang n).
Hypothesen:
H1: Es liegt 1. Wahl vor, d. h. \(p_1 = 10\ \%\).
H2: Es liegt 2. Wahl vor, d. h. \(p_2 = 30\ \%\).
Der Stichprobenumfang sei n = 10.
Wenn von den 10 geprüften Stücken höchstens 2 Ausschussstücke sind, entscheiden wir uns dafür, der Schachtel den Aufkleber „1. Wahl“ zu geben, andernfalls entscheiden wir uns für „2. Wahl“.
Entscheidungsregel:
\(X \leq 2\): Entscheidung für H1
\(X > 2\): Entscheidung für H2
Die Menge A = {0, 1, 2} ist dann der Annahmebereich für H1 und der Ablehnungsbereich für H2, entsprechend ist \(\bar{A}\) ={3, 4, …, 10} der Ablehnungsbereich für H1 und der Annahmebereich für H2.
Bezüglich der Fehler 1. und 2. Art (\(\alpha\)- und \(\beta\)-Fehler) und der entsprechenden Sicherheitswahrscheinlichkeiten (Sicherheiten 1 – \(\alpha\) und 1 – \(\beta\)) sind nun vier Fälle möglich:
Die Wahrscheinlichkeiten \(p_1 = 10\ \%\) bzw. \(p_2 = 30\ \%\) werden beim Ziehen der Stichprobe als konstant betrachtet, also X als binomialverteilt angenommen. Mit \(P_{n; p} (X = k) = B_{n; p} (k)\) gilt:
Sicherheitswahrscheinlichkeit \(1.\) Art: \(P_{10; 0,1} (X \leq 2) = \sum_{i=0}^2 B_{10; 0,1} (i) = 93,0 \%\)
Fehler \(1.\) Art: \(\alpha = P_{10; 0,1} (X > 2) = 1 - P_{10; 0,1} (X \leq 2) = 7,0 \%\)
Fehler 2. Art: \(\beta = P_{10; 0,3} (X \leq 2) = \sum_{i=0}^2 B_{10; 0,3} (i) = 38,3 \%\)
Sicherheitswahrscheinlichkeit 2. Art: \(P_{10; 0,3} (X > 2) = 1 - P_{10; 0,3} (X \leq 2) = 61,7 \%\)