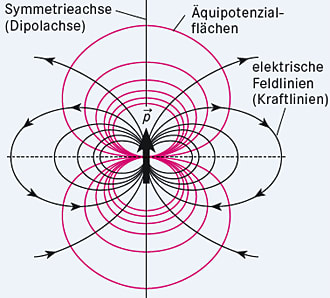
Ein elektrischer Dipol (von griech. di- „zwei-“) ist eine Anordnung von zwei gleich großen, ungleichnamigen Punktladungen in einem Abstand d. Das von ihnen erzeugte elektrische Feld heißt Dipolfeld. Symmetrische Anordnungen von vier oder acht Quellen heißen Quadrupol bzw. Oktupol. Man kann ein beliebiges elektrisches Feld als eine Summe von Multipolfeldern mit zunehmender Ordnung darstellen. Sind die höheren Terme kleine, ist ein Dipol- und-/oder Quadrupolfeld eine Näherung für die unbekannte exakte Feldverteilung.
Wenn die Ladungen eines Dipols \(\pm Q\) betragen, nennt man das Produkt aus Ladung und Abstandsvektor \(\vec d\) das elektrische Dipolmoment \(\vec p\) dieser Anordnung:
\(\vec p = Q \cdot \vec d\)
Die SI-Einheit des Dipolmoments ist Coulomb mal Meter (Cm). Das elektrische Feld in der Umgebung eines elektrischen Dipols wird in Vektorform beschrieben durch
\(\vec E(\vec r) = \dfrac 1 {4\pi\epsilon_0\cdot r^3} \cdot \left[ \left( 3\vec p \cdot \vec r \right) \cdot \dfrac{\vec r}{r^2} - \vec p \right] \)
(\(\vec E\): elektrische Feldstärke, \(\epsilon_0\): elektrische Feldkonstante, \(\vec r\): Ortsvektor des betrachteten Punkts (wenn der Koordinatenursprung in der Mitte des Dipols liegt), \(\vec p \cdot \vec r\): Skalarprodukt der Vektoren \(\vec p\) und \(\vec r\)). Man erkennt, dass die Feldstärke senkrecht zur Richtung des Dipolmoments minimal ist (das Skalarprodukt \(\vec p \cdot \vec r\) ist null, wenn die beiden Vektoren senkrecht aufeinanderstehen) und dass \(\vec E\) für große Abstände proportional zur dritten Potenz des Abstands vom Dipol abnimmt: \(\vec E \sim \dfrac 1 {r^3} \) (das elektrische Feld einer Punktladung nimmt dagegen proportional zum Abstandsquadrat von der Punktladung ab, ein Quadrupolfeld wie \(\dfrac 1 {r^4} \)).
Wenn sich ein elektrischer Dipol in einem äußeren elektrischen Feld \(\vec E\) befindet, über dieses ein Drehmoment \(\vec M = \vec p \times \vec E\) aus, das ihn in Feldrichtung zu drehen versucht.
Die elektrische potenzielle Energie des Dipols im Feld \(\vec E\) beträgt \(E_\text{pot} = -\vec p \cdot \vec E\).
Das magnetische Äquivalent zum elektrischen Dipolmoment ist das magnetische Moment.