-
Aufgabe 1
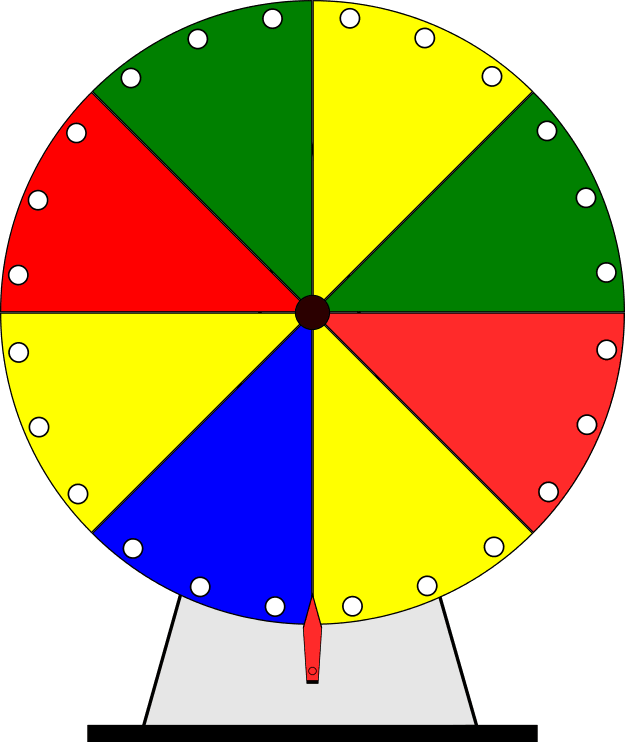
Dauer: 7 Minuten 5 PunkteDas abgebildete Glücksrad wird gedreht. Berechne die Wahrscheinlichkeit, dass die Farbe, auf der der Zeiger stehen bleibt, …
- blau ist.
- gelb ist.
- grün oder rot ist.
- nicht grün ist.
- nicht gelb ist.
-
Aufgabe 2
Dauer: 6 Minuten 4 PunkteEin Autohändler bietet 5 verschiedene Fahrzeugmodelle an. Jedes Modell gibt es in 8 verschiedenen Farben. Zusätzlich kann ein Kunde bei der Ausstattung zwischen „Standard“, „Komfort“ und „Premium“ wählen.
- Bestimme, wie viele verschiedene Möglichkeiten ein Kunde hat, ein Auto auszuwählen.
- Herr Schick möchte ein schwarzes Auto kaufen. Aus wie vielen Möglichkeiten kann er wählen?
-
Aufgabe 3
Dauer: 4 Minuten 3 PunkteElias hat im Urlaub 40 Fotos gemacht. Davon möchte er 3 vergrößert an die Wand hängen. Bestimme, wie viele Möglichkeiten Elias hat, 3 Fotos auszuwählen.
-
Aufgabe 4
Dauer: 6 Minuten 5 PunkteIn einer Tüte sind 8 rote und 5 weiße Schokolinsen. Pia sagt: „Die Wahrscheinlichkeit, zufällig eine rote Schokolinse zu ziehen, ist \(\frac{8}{13}\).“
Dagegen meint Jakob: „Das kann man so nicht rechnen, das ist kein Laplace-Experiment. Die Wahrscheinlichkeiten für eine rote Linse und für eine weiße Linse sind nicht gleich groß. Es gibt ja mehr rote Linsen.“Wer von beiden hat recht? Begründe deine Meinung.
-
Aufgabe 5
Dauer: 15 Minuten 10 PunkteLouisa und 7 weitere Mädchen spielen in einem Volleyballteam. Aber nur 6 von ihnen dürfen mitspielen.
- Bestimme, wie viele Möglichkeiten die Trainerin hat, 6 Spielerinnen aus dem Team auszuwählen.
- Bestimme, bei wie vielen der Möglichkeiten aus Aufgabe a Louisa dabei ist.
- Würde die Trainerin auslosen, wer mitspielen darf, wie groß wäre dann die Wahrscheinlichkeit, dass Louisa dabei ist? Louisa überlegt: „Da 6 von 8 mitspielen, müsste die Wahrscheinlichkeit \(\frac68=75\ \%\) sein.“ Überprüfe Louisas Überlegung mithilfe der Ergebnisse aus den Aufgaben a und b.
- Da Sophie in Topform ist, soll sie auf jeden Fall spielen. Amelie soll dagegen nicht spielen, da sie leicht verletzt ist. Bestimme, wie viele Möglichkeiten es nun gibt, die weiteren Spielerinnen für das Spiel auszuwählen.
- Bestimme unter den Bedingungen aus Aufgabe d die Wahrscheinlichkeit, dass Louisa spielt, wenn unter den weiteren Spielerinnen gelost wird.
-
Aufgabe 6
Dauer: 6 Minuten 3 Punkte- 5 Personen nehmen an einem Tischtennisturnier teil, bei dem jeder Spieler einmal gegen jeden anderen spielt. Bestimme, wie viele Spiele es insgesamt gibt.
- Bestimme einen Term, der die Gesamtzahl der Spiele angibt, wenn n Personen an dem Turnier teilnehmen.
-
Aufgabe 1
Das abgebildete Glücksrad wird gedreht. Berechne die Wahrscheinlichkeit, dass die Farbe, auf der der Zeiger stehen bleibt, …
- blau ist.
- gelb ist.
- grün oder rot ist.
- nicht grün ist.
- nicht gelb ist.