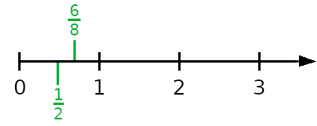Was du wissen musst
-
Welche Eigenschaften von Brüchen sind beim Vergleichen und ordnen wichtig?
Brüche bestehen aus drei Teilen:
- Zähler
- Nenner
- Bruchstrich
Der Bruchstrich zeigt, dass es sich bei der vorhanden Zahl um einen Bruch handelt. Die anderen beiden Elemente geben Auskunft über die Größe der Zahl.
Der Nenner gibt an, in wie viele Teile ein Ganzes geteilt wird. Im Fall von \(\frac{3}{4}\) bedeutet das, dass etwas in \(4\) Teile geteilt wurde. Brüche lassen sich am besten vergleichen, wenn sie gleichnamig sind. Dass bedeutet, dass die betreffenden Brüche denselben Nenner haben. So sind \(\frac{1}{4}\) und \(\frac{3}{4}\) gleichnamig, \(\frac{3}{6}\) und \(\frac{3}{4}\) aber nicht. Um sie gleichnamig zu machen, musst du entweder kürzen oder erweitern. Dabei kann es passieren, dass zwei Brüche gleich groß sind, obwohl sie auf den ersten Blick unterschiedlich aussehen. Das haben wir schon in der Einleitung bei \(\frac{2}{4}\) und \(\frac{1}{2}\) gesehen.
Der Zähler gibt Auskunft über die Anzahl der Teile einer Bruches. Dieser steht immer über dem Bruchstrich und hat beim Bruch \(\frac{3}{4}\) die Größe \(3\). Er muss betrachtet werden, um gleichnamige Brüche zu vergleichen.
-
Wie vergleicht man Brüche miteinander?
Um Brüche miteinander zu vergleichen, musst du erst die
- Gleichnamigkeit prüfen.
Gegebenenfalls muss du diese dann
Sind die Brüche schon gleichnamig, kannst du den zweiten Schritt überspringen. Zu guter Letzt werden die
- Zähler verglichen.
Ein wichtiger Sonderfall ist der gemischte Bruch. Hierbei musst du auch die ganzen Teile in den nachgestellten Bruch mit einbringen.
-
Wie stellt man geordnete Brüche dar?
Geordnete Brüche lassen sich am Zahlenstrahl oder mit sogenannten Ordnungsrelationen \(\left( <, \leq, \geq, > \right)\) darstellen.
Wir schauen uns das am Beispiel \(\frac{1}{2}\) und \(\frac{6}{8}\) an. Das sind ungleichnamige Brüche, für die \(\frac{1}{2} = \frac{2}{4}\) und \(\frac{6}{8} = \frac{3}{4}\) gilt. Durch das Vergleichen der Zähler erkennen wir, dass \(\frac{1}{2}\) kleiner als \(\frac{6}{8}\) ist.
Das kann man auch mit dem Symbol \(<\) (sprich: „kleiner als“) aufschreiben: \(\frac{1}{2} < \frac{6}{8}\). Am Zahlenstrahl ist das Ganze anschaulicher. Trage die Werte dazu an den richtigen Stellen ein. Je weiter links eine Zahl auf dem Strahl ist, desto kleiner ist sie.
-
Wozu muss man Brüche ordnen?
Brüche spielen wie jeder andere Zahlentyp im Alltag eine große Rolle. In den USA hat sich jedoch etwas ereignet, dass noch einmal die Wichtigkeit des Zahlenordnens unterstreicht. So hatten zwei konkurrierende Fast-Food-Ketten den gleichen Burger zum selben Preis. Der einzige Unterschied war, dass der eine Burger mehr wog als der andere:
- einer wog \(\frac{1}{3}\) Pfund (\(\approx 151{,}2 \text{ g}\))
- der andere wog \(\frac{1}{4}\) Pfund (\(\approx 113{,}4 \text{ g}\))
Die Kunden haben aber immer den kleineren gekauft. Das lag unter anderem daran, dass sie \(\frac{1}{4}\) für größer als \(\frac{1}{3}\) hielten. Zwar gab es sicherlich auch andere Gründe, doch ändert das nichts an dem grundlegenden Fehler, der gemacht wurde. Damit dir so was nicht passiert, solltest du Brüche auf jeden Fall ordnen können. Denn trügerische Angaben werden nicht nur bei Fast Food gemacht.