Die einfachen Zahlzeichen
Die lateinischen Zahlzeichen wurden nach mehreren verschiedenen Systemen gebildet, in denen aber die Zahlen unter 1'000 gleich dargestellt wurden. Die folgende Tabelle gibt die Grundzeichen von jedem dieser Systeme in einer eigenen Spalte an.
Erläuterungen zur Tabelle
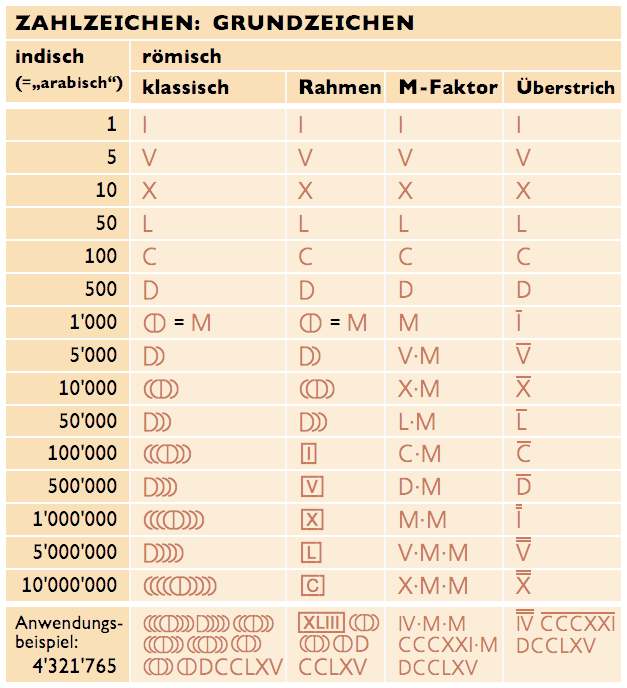
• Die erste Spalte („indisch“) enthält Zahlen nach unserem heutigen Zahlsystem. Wir nennen es meist „arabische Zahlen“. Die korrekte Bezeichnung ist jedoch „indische Zahlen“, da sie von den Indern stammen, die um 500 n.Chr. das Dezimalsystem erfanden. Nachdem diese Zahlen von den Arabern übernommen worden waren, lernten die Europäer sie von den Arabern kennen.
• Die zweite Spalte („römisch – klassisch“) zeigt die ältere römische Schreibweise. Einfache Zahlzeichen gibt es nur für die hier dargestellten Zahlen. Für 2, 3, 4 und 6, 7, 8, 9 mussten zusammengesetzte Zeichen gebildet werden, ebenso für die Zahlen zwischen 10 und 50 usw. Diese findest du mithilfe der Tabelle unten. Beachte die Herkunft der Zeichen:
• C = 100 ist die Abkürzung für centum.
• M = 1'000 ist die Abkürzung für mille. Das gleichbedeutende Ø-ähnliche Zeichen ist älter und dient zur Ableitung der höherwertigen Zahlzeichen.
Alle Zeichen für fünffache Zehnerpotenzen (5, 50, 500 usw.) sind durch Halbierung der nächsten Zehnerpotenz (10, 100, 1'000 usw.) entstanden:
• V = 5 ist die obere Hälfte von X = 10.
• L = 50 ist die eckig geschriebene untere Hälfte von C = 100.
• D ist die rechte Hälfte des Ø-ähnlichen Zeichens für 1'000.
Ebenso bedeutet auch bei den übrigen Zeichen die Halbierung des Zeichens immer den halben Wert.
• Die dritte Spalte („römisch – Rahmen“) stimmt bis 50'000 mit der vorherigen Spalte überein. Für die höheren Zahlen werden die Zeichen der niedrigen Zahlen I, V, X usw. wiederverwendet, aber mit einem Rahmen umgeben. Der Rahmen bedeutet, dass der Zahlwert der darinstehenden Zeichen mit 100'000 multipliziert werden muss. Dieses System erfanden die Römer, weil das ältere System für die Schreibung hoher Zahlen zu unübersichtlich war. Das Anwendungsbeispiel in der Tabelle zeigt, wie viel leserlicher mit dem neuen System geschrieben und wie viel Platz eingespart werden konnte. Der Rahmen konnte ein geschlossenes Rechteck aus vier Linien sein, es konnte aber auch die untere Linie oder die obere und die untere Linie fehlen.
• Die vierte Spalte („römisch – M-Faktor“) enthält ein System, das die Römer seltener gebrauchten, obwohl es einfach und übersichtlich ist. Hier werden die höheren Zahlen dadurch gebildet, dass man an die niedrigeren Zahlen ·M (= mīlia Tausende) anhängt. Dass bedeutet, dass die niedrigeren Zahlen mit 1'000 multipliziert werden, wie es bei den Zahlwörtern ja auch ist; z.B.:
÷ C·M = Centum Mīlia hundert Tausende = hunderttausend.
Ab 1 Million muss zweimal mit tausend multipliziert werden, also ·M·M („Mīlia Mīlium“), ab 1 Milliarde dreimal, also ·M·M·M („Mīlle Mīlia Mīlium“). Da ·M·M als Zahl 2'000 und ·M·M·M als Zahl 3'000 missverstanden werden konnte, bevorzugte man für hohe Zahlen das System mit den Rahmen.
• Die fünfte Spalte („römisch – Überstrich“) zeigt ein sehr übersichtliches System, das aber erst im Mittelalter erfunden wurde. Es funktioniert im Prinzip wie das System mit dem M-Faktor, jedoch wird die Multiplikation mit 1000 nicht durch ein nachgestelltes ·M, sondern durch einen übergesetzten Strich angezeigt. Für die Millionen gebraucht man statt zwei nachgestellter ·M zwei übergesetzte Striche. Im Altertum konnten die Römer ein solches System nicht verwenden, da der übergesetzte Strich eine andere Funktion hatte: Er zeigte an, dass die Buchstaben nicht als Wörter oder Abkürzungen für Wörter, sondern als Zahlen zu verstehen waren.
Bildung zusammengesetzter Zahlen mittels Tabelle
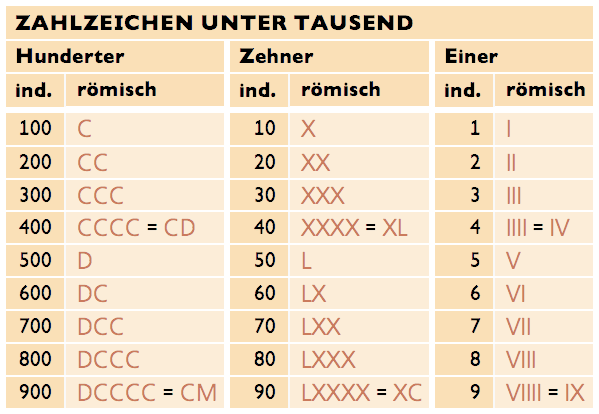
Alle Zahlen, für die es kein einfaches Zeichen gibt, müssen als Kombination von mehreren Zeichen dargestellt werden. Die Zahlen von 1 bis 999 kannst du ganz einfach mithilfe der Tabelle oben bilden.
• Zuerst zerlegst du die Zahl in Hunderter, Zehner und Einer, z.B.:
736 = 700 + 30 + 6.
• Dann ersetzest du die so gewonnenen Zahlen durch die Zahlzeichen aus der Tabelle:
700 = DCC
30 = XXX
6 = VI
• Schließlich setzest du die römischen Zahlen zu einer einzigen zusammen. Ergebnis:
763 = DCCXXXVI
Beachte: Wo in der Tabelle ein Gleichheitszeichen steht, kannst du zwischen einer längeren und einer kürzeren Schreibweise auswählen. Die kürzere gilt als eleganter. Bei der kürzeren Schreibweise steht ein geringerwertiges Zeichen vor einem höherwertigen. Das bedeutet immer, dass der geringere Wert von dem höheren abgezogen wird, also:
CD = D – C = 500 – 100 = 400
CM = M – C = 1000 – 100 = 900
XL = L – X = 50 – 10 = 40
XC = C – X = 100 – 10 = 90
IV = V – I = 5 – 1 = 4
IX = X – I = 10 – 1 = 9
Regeln für die Bildung zusammengesetzter Zahlen
(1) ERSTER SCHRITT
(1a) Wir haben folgenden Bestand an Zahlzeichen:
• Es gibt eine Serie von Zeichen, bei denen sich, von 1 ausgehend, der Wert jeweils auf das Zehnfache erhöht:
I = 1,
X = 10,
C = 100,
M = 1000,
usw.
Wir nennen die Zeichen der ersten Serie Vollwertzeichen.
• Zu jedem dieser Zeichen, mit Ausnahme von I = 1, gibt es ein weiteres mit dem halben Wert. So erhalten wir eine zweite Serie:
V = 5 (= Hälfte von 10),
L = 50 (= Hälfte von 100),
D = 500 (= Hälfte von 1000),
usw.
Wir nennen die Zeichen der zweiten Serie Halbwertzeichen.
(1b) Von der Zahl, die man schreiben will, zieht man die größte einfache römische Zahl ab, die darin enthalten ist, und schreibt deren Zeichen auf.
Z.B.: Nehmen wir an, dass wir den Zahlwert 736 schreiben wollen.
• Von 736 lässt sich höchstens D = 500 abziehen, also schreiben wir: D
• Es bleibt ein Rest von 236.
(1c) Das Verfahren von Nummer (1b) wird so oft wiederholt, bis der gesamte Betrag der Zahl verbraucht ist, also:
• Aus Nummer (1b) haben wir schon: D
• Von dem Rest 236 lässt sich höchstens C = 100 abziehen, wir schreiben: C
• Von dem Rest 136 lässt sich höchstens C = 100 abziehen, wir schreiben: C
• Von dem Rest 36 lässt sich höchstens X = 10 abziehen, wir schreiben: X
• Von dem Rest 26 lässt sich höchstens X = 10 abziehen, wir schreiben: X
• Von dem Rest 16 lässt sich höchstens X = 10 abziehen, wir schreiben: X
• Von dem Rest 6 lässt sich höchstens V = 5 abziehen, wir schreiben: V
• Von dem Rest 1 lässt sich höchstens I = 1 abziehen, wir schreiben: I
(1d) Die dabei notierten römischen Zahlen werden aneinandergehängt. Ergebnis:
DCCXXXVI
Beachte, dass das Ergebnis mit folgenden Regeln übereinstimmen muss:
• Alle Zahlzeichen sind vom höchsten zum niedrigsten Wert geordnet.
• Kein Zeichen kommt mehr als viermal vor.
• Kein Halbwertzeichen (V, L, D usw.) kommt mehr als einmal vor.
(2) ZWEITER SCHRITT: Vereinfachung durch Subtraktionsregel
Dieser zweite Schritt ist heutzutage beim Schreiben römischer Zahlen üblich, um die Zahlen zu verkürzen. Die Römer selber gaben sich meistens mit dem Ergebnis des ersten Schritts zufrieden!
(2a) Wenn im Ergebnis des ersten Schritts ein Zeichen viermal vorkommt, darf es durch eine einfachere Schreibweise ersetzt werden.
Z.B.: Nehmen wir an, das Ergebnis des ersten Schritts wäre 429 = CCCCXXVIIII.
• Wir suchen für jedes viermalige Zeichen sein nächsthöheres Zeichen.
CCCC > D
IIII > V
• Wir setzen das Zeichen, das ursprünglich viermal vorkam, ein einziges Mal vor das höhere Zeichen.
CCCC = CD
IIII = IV
Auf diese Weise steht ein geringeres Zeichen vor einem höheren (was sonst nicht erlaubt ist!).
Das bedeutet, dass das niedrigere von dem höheren abgezogen wird (Subtraktionsregel).
CD = D – C = CCCC (bedeutet: 500 – 100 = 400)
IV = V – I = IIII (bedeutet: 5 – 1 = 4)
• Ergebnis: 429 = CDXXVIV,
Problem: Zwei V sind nicht erlaubt!
(2b) Wenn im Ergebnis von (2a) ein Halbwertzeichen doppelt vorkommt, muss nochmals ersetzt werden:
• Die beiden Halbwertzeichen werden zum nächsthöheren Vollwertzeichen zusammengerechnet.
V + V = X
• Die beiden Halbwertzeichen werden herausgenommen und durch dieses Vollwertzeichen ersetzt, wir setzen es in unserer Zahl an die Stelle des zweiten Halbwertzeichens.
CDXXVIV > CDXX IX
Auch das bedeutet wieder, dass ein geringeres Zeichen vor einem höheren steht, also sein Wert von diesem abgezogen wird:
IX = X – I = VIIII (bedeutet: 10 – 1 = 9)
• Ergebnis:
429 = CDXXIX.