Linse

In der Optik ist eine Linse ein meist scheibenförmiger, von gekrümmten Oberflächen begrenzter durchsichtiger Körper (meist aus Glas oder Kunststoff), mit dem sich die geradlinige Ausbreitung von Lichtstrahlen beeinflussen lässt. Analog nennt man in der Elektronenoptik Bauteile, die Elektronen oder allgemeiner geladene Teilchenstrahlen ablenken können, (Elektronen-)Linsen. Die Wirkungsweise von optischen Linsen beruht auf der Brechung.

Die Form einer Linse kann sehr kompliziert sein (etwa Brillengläser). In der Schulphysik hat man es meist mit sphärischen Linsen zu tun, die entweder von Teilen von Kugeloberflächen oder von Ebenen begrenzt sind. Die Mittelpunkte der Kugelflächen bezeichnet man als Krümmungsmittelpunkte, ihre Verbindungslinie definiert die optische Achse der Linse. Die Radien der Kugelflächen heißen die Krümmungsradien r₁ und r₂ (bei einer ebenen Grenzfläche ist der Krümmungsradius \(r = \infty\)). Stimmen beide Krümmungsradien überein, spricht man von einer symmetrischen Linse, sonst von asymmetrischen Linsen. Die Ebene, die senkrecht zur optischen Achse steht und durch den Schnitt der beiden Kugelflächen bestimmt wird, heißt Linsenebene. Bei symmetrischen Linsen ist sie gleichzeitig die Symmetrieebene der Linse.

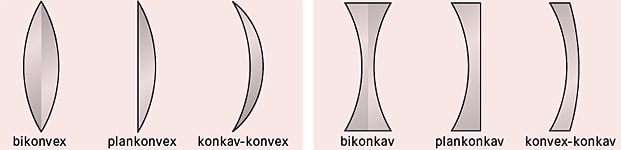
Linsen, die in der Mitte dicker sind als am Rand, nennt man Konvexlinsen, Linsen, die in der Mitte dünner sind als am Rand, werden als Konkavlinsen bezeichnet (Abb.). Ist das Linsenmaterial optisch dichter als die Umgebung (z. B. Glaslinse in Luft), dann wirkt eine Konvexlinse als Sammellinse, eine Konkavlinse dagegen als Zerstreuungslinse.

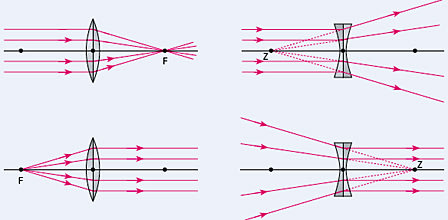
Die wichtigste Größe einer Linse ist die Brennweite f. Sie gibt den Abstand der Brennpunkte F_{1, 2} (bzw. der virtuellen Brennpunkte oder Zerstreuungspunkte Z_{1, 2}) von der Linsenebene an (Abb.). Für den Zusammenhang zwischen der Brennweite einer Linse und den Krümmungsradien gilt die Linsenformel.

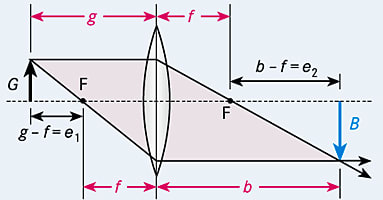
Man verwendet Linsen zur optischen Abbildung. Der Zusammenhang zwischen der Brennweite f, dem Abstand des Gegenstands von der Linse (Gegenstandsweite g) und dem Abstand des Bildes von der Linse (Bildweite b) wird durch die Abbildungsgleichungen angegeben. Diese haben für nicht zu achsenferne Strahlen die Form

\(\dfrac 1 g + \dfrac 1 b = \dfrac 1 f\)

(g: Gegenstandsweite, b: Bildweite). Für die Entfernungen von Gegenstand und Bild vom Brennpunkt, e_G und e_B, gilt die Gleichung

\(e_\text G \cdot e_\text B = f^2\)

Bei der zeichnerischen Konstruktion der Bilder versucht man, die Strahlengänge auf die Brechung an einer Ebene, der Linsenebene, zurückzuführen. Ist dies möglich, so spricht man von einer dünnen Linse. In der Schule werden durchweg dünne Linsen benutzt. Spielt dagegen die Dicke der Linse eine Rolle, sodass diese Vereinfachung nicht mehr möglich ist, spricht man von einer dicken Linse. Hier muss man zwei Hauptebenen H₁ und H₂ unterscheiden.

Vereinigt man mehrere Linsen zu einem einzigen abbildenden System, um Abbildungsfehler auszugleichen oder die Brennweite zu verändern (Zoomlinse), spricht man vom einem Linsensystem. In der Regel haben die Linsen im System eine gemeinsame optische Achse.

Übrigens: Der Name „Linse“ für das optische Element kommt im Deutschen wie im Lateinischen von den „linsenförmigen“ Gemüselinsen.