• Aufgabe 1

    2 Minuten 3 Punkte
    einfach

    Schreibe die drei Größengleichungen auf, mit denen sich \(s\), \(v\) und \(t\) bei einer geradlinigen, gleichförmigen Bewegung aus den jeweils anderen beiden Größen berechnen lassen.

  • Aufgabe 2

    1 Minute 2 Punkte
    mittel

    Ordne die folgenden Einheiten einer physikalischen Größe zu:

    1. \(\text{mm}\)
    2. \(\frac{\text{cm}}{\text{Min}}\)

  • Aufgabe 3

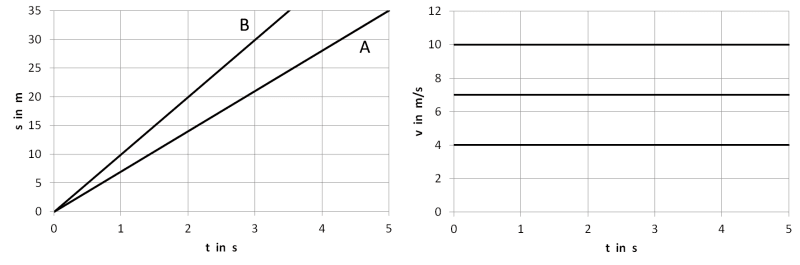
    6 Minuten 4 Punkte
    mittel
    1. Betrachte die \(s\)-\(t\)-Kurven im linken Diagramm. Ordne sie den \(v\)-\(t\)-Kurven im rechten Diagramm korrekt zu, indem du dort die Graphen gleichermaßen mit A bzw. B benennst.
    2. Eine der \(v\)-\(t\)-Kurven gehört weder zu A noch zu B. Nenne sie C und zeichne die ihr zugehörige \(s\)-\(t\)-Kurve im linken Diagramm ein.

     


     

  • Aufgabe 4

    17 Minuten 14 Punkte
    mittel

    Der sogenannte Ironman ist ein sportlicher Wettkampf bestehend aus den Sportarten Schwimmen, Radfahren und Laufen. Betrachte den \(s\)-\(t\)-Verlauf und den \(v\)-\(t\)-Verlauf eines Athleten beim Ironman.

     


    1. Berechne anhand des \(s\)-\(t\)-Diagramms die jeweiligen Geschwindigkeiten in den ersten beiden Etappen (Schwimmen und Radfahren) sowie anhand des \(v\)-\(t\)-Diagramms die zurückgelegte Strecke in der letzten Etappe (Laufen).
    2. Vervollständige nun die Diagramme. Ergänze also die Etappen Schwimmen und Radfahren im \(v\)-\(t\)-Diagramm und die Etappe Laufen im \(s\)-\(t\)-Diagramm.
    3. Berechne die Durchschnittsgeschwindigkeit für den gesamten Wettkampf.

  • Aufgabe 5

    10 Minuten 7 Punkte
    schwer
    1. Schreibe eine kurze Geschichte zu einer Bewegung, die dem abgebildeten \(s\)-\(t\)-Diagramm entspricht. Achte darauf, auf die wesentlichen Aspekte der Kurve einzugehen. 
    2. Ermittle den Unterschied zwischen der tatsächlichen Ankunftszeit und der Ankunftszeit bei \(3\,\text{km}\), wenn die Bewegung unverändert mit der Anfangsgeschwindigkeit weitergegangen wäre. 

     


     

  • Aufgabe 6

    5 Minuten 3 Punkte
    schwer

     


    1. Gib ein Beispiel für eine Bewegung an, die zu dieser \(s\)-\(t\)-Kurve führen könnte.
    2. Schätze den Wert der Maximalgeschwindigkeit der Bewegung ab.