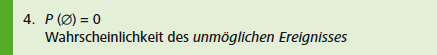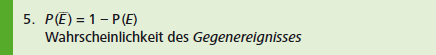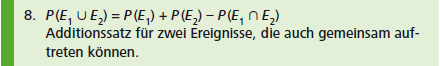Erklärung: Die Anzahl der günstigen Ergebnisse (Zähler) ist immer kleiner oder gleich der Anzahl der möglichen Ergebnisse (Nenner).
BEISPIEL Werfen eines Würfels: \(P (\{1~ f\ddot{a}llt, 6 ~f\ddot{a}llt\}) = \frac{2}{6} = \frac{1}{3} = P (\{1~ f\ddot{a}llt\}) + P (\{6 ~f\ddot{a}llt\}) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}\)
BEISPIEL Werfen eines Würfels: \(P (Augenzahl < 7) = \frac{6}{6} = 1\)
BEISPIEL Werfen eines Würfels: \(P (Augenzahl > 7) = \frac{0}{6} = 0\)
BEISPIEL Werfen eines Würfels: \(P (keine~ 4~ oder~ 5):\)
\(E = \{4; 5\}; P (E) = \frac{2}{6} = \frac{1}{3}\) \(P (\overline{E}) = 1 - \frac{1}{3} = \frac{2}{3}\)
BEISPIEL \(E_1 = \{Augenzahl\) \(teilbar\) \(durch\) \(4\} = {4}\) ; \(E_2 = \{gerade\) \(Augenzahl\} = \{2, 4, 6\}\) ; \(E_1 \subseteq E_2\) ; \(\frac{1}{6} = P ( E_1 ) \leq P ( E_2 ) = \frac{3}{6} = \frac{1}{2}\)
BEISPIEL \(E_1 = \{2~ f\ddot{a}llt\}\) ; \(E_2 = \{ungerade\) \(Augenzahl\}\) ; \(E_1 \cap E_2 = ∅\) ; \(P ( E_1 \cup E_2 ) = P ( E_1 ) + P ( E_2 ) = \frac{1}{6} + \frac{3}{6} = \frac{4}{6} = \frac{2}{3}\)
BEISPIEL \(E_1 = \{4~ f\ddot{a}llt\}\) ; \(E_2 = \{gerade\) \(Augenzahl\}\) ; \(E_1 \cap E_2 = \{4~ f\ddot{a}llt\}\) ; \(P ( E_1 \cup E_2 ) = \frac{1}{6} + \frac{3}{6} - \frac{1}{6} = \frac{3}{6} = \frac{1}{2}\)