-
Aufgabe 1
Dauer: 6 Minuten 4 PunkteGegeben sind die Buchstaben E, F, H, I, M, N.
- Welche der Buchstaben sind achsensymmetrisch?
- Welche der Buchstaben sind punktsymmetrisch?
-
Aufgabe 2
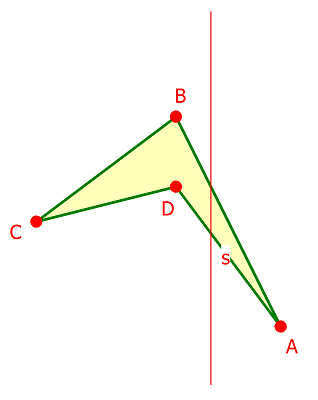
Dauer: 8 Minuten 5 PunkteKonstruiere das Bild des Vierecks ABCD, das bei der Spiegelung an der Achse s entsteht.
-
Aufgabe 3
Dauer: 10 Minuten 6 PunkteZeichne die Punkte A(-2|1), B(-2,5|-2), C(1|-1) und Z(2|1) in ein Koordinatensystem ein und spiegele die Punkte A, B und C an Z.
-
Aufgabe 4
Dauer: 8 Minuten 6 PunkteZeichne die Punkte P(4|1) und P'(5|4) in ein Koordinatensystem. Konstruiere die Spiegelachse s so, dass der Punkt P' das Bild von P ist, wenn man den Punkt P an der Spiegelachse s spiegelt.
-
Aufgabe 5
Dauer: 7 Minuten 6 PunkteEin Rechteck mit den Eckpunkten A, B, C und D wird am Zentrum Z gespiegelt. Wo muss Z liegen, damit ...
- ... der Bildpunkt von A auf dem Punkt B zu liegen kommt?
- ... der Bildpunkt von C wieder auf dem Punkt C zu liegen kommt?
- ... der Bildpunkt von A auf dem Punkt D zu liegen kommt?
-
Aufgabe 6
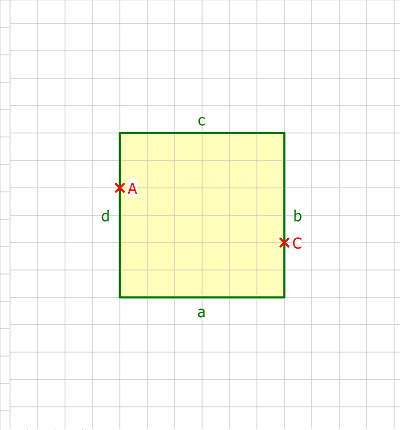
Dauer: 6 Minuten 3 PunkteIn dem folgenden Quadrat liegen der Punkt A auf der Seite d und der Punkt C auf der Seiten b. Wo muss der Punkt B auf der Seite a und der Punkt D auf der Seite c liegen, damit das Viereck ABCD einen möglichst kleinen Umfang besitzt? Löse das Problem durch eine Konstruktion.
-
Aufgabe 1
Gegeben sind die Buchstaben E, F, H, I, M, N.
- Welche der Buchstaben sind achsensymmetrisch?
- Welche der Buchstaben sind punktsymmetrisch?